何叨叨的个人博客算法
动态规划
介绍
动态规划（Dynamic Programming，简称DP）
动态规划的特点：
- 具有重叠子问题
- 最优子结构
- 状态转移方程
动态规划的解题方法：
- 递归+记忆化(自顶向下)
- 动态规划（自底向上）
解动态规划题目的步骤：
- 根据重叠子问题定义状态
- 寻找最优子结构推导状态转移方程
- 确定dp初始状态
- 确定输出值
斐波那契
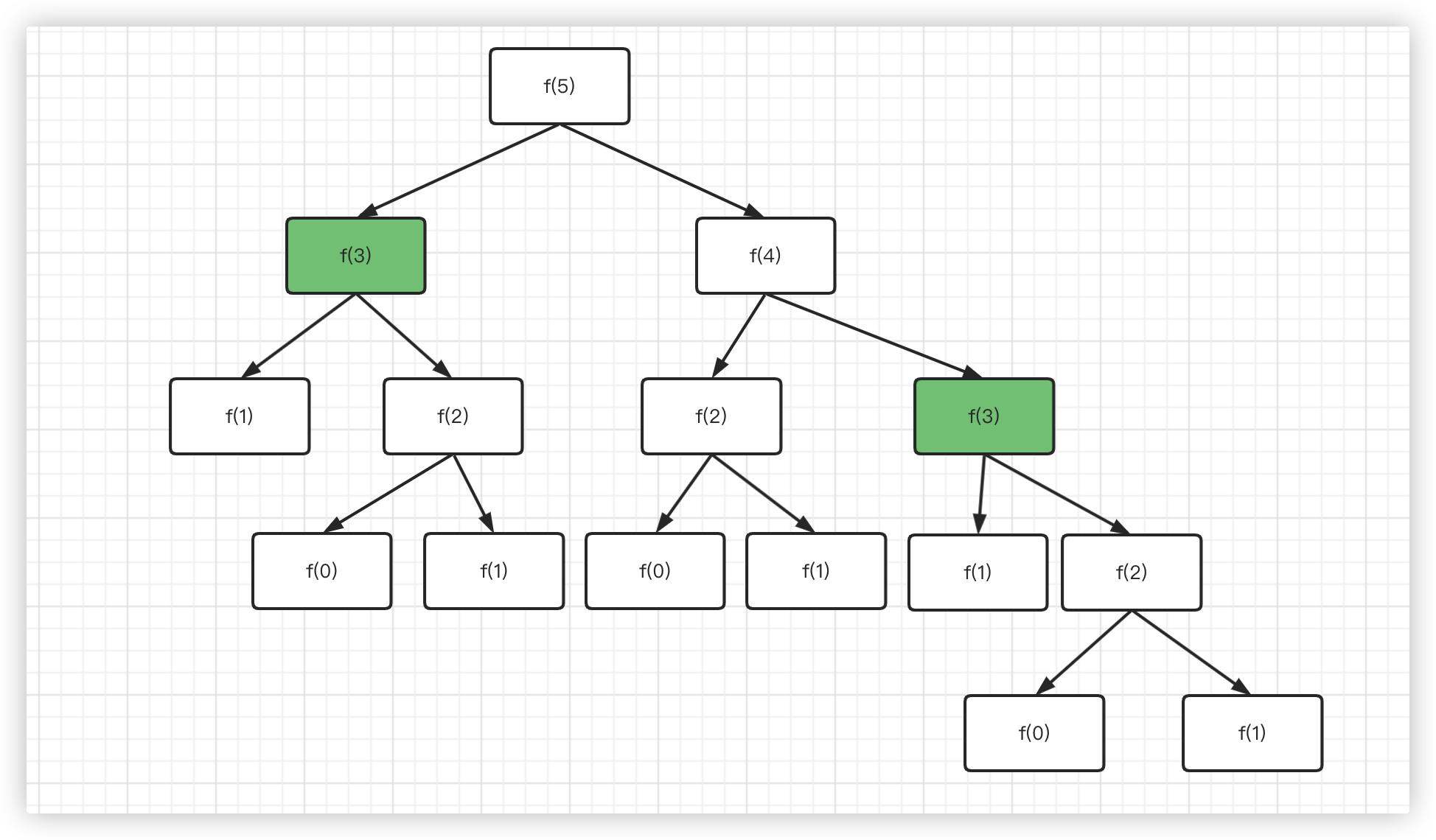
自顶向下：
递归
jsvar fib = function(n) { if(n===0){ return 0 } if(n===1){ return 1 } return fib(n-2)+fib(n-1) };递归+记忆化
单纯的递归效率较低，例如图中的绿色部分f(3)会多次计算。所以将运算结果存储下来，会进一步提高效率
使用数据将f(n)的值存在res[n]中
jsvar fib = function(n) { let res=[0,1] if(n===0){ return 0 } if(n===1){ return 1 } if(res[n]!==undefined){ return res[n] } res[n]=fib(n-2)+fib(n-1) return res[n] };
自底向上（动态规划）：
常规解法
dp数组保存了从0到n中所有斐波那契数，而实际上我们只需要f(n)。那就可以将o(n)的空间复杂度继续优化
jsvar fib = function(n) { if(n<=1){ return n } //dp初始状态 let dp=[0,1] for(let i=2;i<=n;i++){ //状态转移方程 dp[i]=dp[i-2]+dp[i-1] } //确定输出值为dp[0] return dp[n] };动态规划的压缩
实际上，只需要保存两个变量即可，pre上一个值，cur当前值
jsvar fib = function(n) { if(n<=1){ return n } let pre=0,cur=1 for(let i=2;i<=n;i++){ [pre,cur]=[cur,pre+cur] //f(2)=f(0)+f(1) , pre=f(0),cur=f(1) //f(3)=f(1)+f(2) , cur=pre+cur } return cur };
不同路径
这题很难看出来是动规划
根据重叠子问题定义状态
到达每个单元格只能是从（左侧+上侧）来的，到达该单元格的路径条数也只能是 （到达左侧单元格的路径条数+到达上侧单元格的路径条数）
寻找最优子结构推导状态转移方程
r是行索引、c是列索引、
dp[r][c]是记录到达该单元格的路径条数dp[r][c]=dp[r-1][c]+dp[r][c-1]确定dp初始状态
第一行的单元格只能=到达左侧单元格的路径条数=1
第一列的单元格只能=到达上侧单元格的路径条数=1
确定输出值
动态规划常规解法： 时间复杂度o(mn) 、 空间复杂度o(mn)
jsvar uniquePaths = function(m, n) { let dp=new Array(m).fill(0).map(()=>{ //语法补充Array(m)必须填充数字，map才能将每个元素替换为数组 return new Array(n).fill(0) }) //初始化第一行，第一列都是1 dp[0]=new Array(n).fill(1) for(let i=0;i<m;i++){ dp[i][0]=1 } //动态规划，自底向上 for(let i=1;i<m;i++){ for(let j=1;j<n;j++){ dp[i][j]=dp[i][j-1]+dp[i-1][j] } } return dp[m-1][n-1] };动态规划的压缩
原本的dp数据是个二维数组，但是这里可以压缩一维数组，每一个dp数组记录的是当前行的单元格的路径数
jsdp[w]=dp[w]+dp[w-1] //w是列索引通过状态转移方程，可以一层一层的向下转移状态。新的绿色的dp[3]=新的绿色的dp[2]+旧的红色的dp[3]
jsvar uniquePaths = function(m, n) { dp=new Array(n).fill(1) for(let i=1;i<m;i++){ for(let j=1;j<n;j++){ dp[j]=dp[j]+dp[j-1] } } return dp[n-1] };
爬楼梯
js
var climbStairs = function(n) {
if(n<=2){
return n
}
let dp=[undefined,1,2] //数组索引就是楼梯阶数，没有0阶楼梯，座所以这里用undefined占位一下
for(let i=3;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2]
}
return dp[n]
};压缩dp数组
js
var climbStairs = function(n) {
if(n<=2){
return n
}
let pre=1
let cur=2
for(let i=3;i<=n;i++){
[cur,pre]=[cur+pre,cur]
}
return cur
};完全平方数
相对于前面的题目，从这题开始，后面的题目全部涉及最优子结构，题目中一般表现为 "最少"、"最小"、"最短"等字眼
根据重叠子问题定义状态
寻找最优子结构推导状态转移方程
n是数，dp[n]存的是和为
n的完全平方数的最少数量dp[n]：初始化为最多的情况，即dp[n]=n（n个1的平方相加）dp[n-j*j]+1：n-j*j这个数的最少平方数+1个平方数(j*j)两者取最小的就是当前n这个数的最小平方数
dp[n]=Math.min(dp[n-j*j]+1,dp[n])确定dp初始状态
dp[n]=n，
这里注意n是从1开始的，
j=1来时循环dp[0]=0和i-j*j>=0这个边界比难理解，假设n=9，其实只需要1个平方数3*3即可，这时候j=3，dp[9-3*3]+1=1确定输出值
dp[n]
js
var numSquares = function(n){
let dp=[]//先把所有位置放置0
for(let i=1;i<=n;i++){
dp[i]=i //初始化为最多的情况，比如：dp[2]=2，就是1^2+1^2,共两个平方数
for(let j=1;i-j*j>=0;j++){
dp[i]=Math.min(dp[i],dp[i-j*j]+1)
}
}
return dp[n]
};三角形最小路径和
这题也涉及最优子结构
js
var minimumTotal = function(triangle) {
//动态规划 dp[n]=min(dp[n],dp[n+1])
let row=triangle.length
let dp=new Array(row).fill(0).map(()=>{
return new Array(triangle[row-1].length)
})
//dp[row-1]=triangle[row-1] 一般不要这样初始化倒数第一行 ，实际上只是把triangle最后一行的指针指向了dp
//可以写成这样
for(let i=row-1;i>=0;i--){ //倒数第一行应该被初始化，从倒数第二行开始计算
for(let j=0;j<triangle[i].length;j++){
if(i===row-1){
dp[i][j]=triangle[i][j]
}else{
dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]
}
}
}
return dp[0][0]
};上面dp数组和参数triangle数组大小一样
因为dp每个元素保存的是到该点的最小路径值，我们只需要第一行的值即可，所以，我们可以压缩为一维数组，不必保存所有的值
js
var minimumTotal = function(triangle) {
//动态规划 dp[n]=min(dp[n],dp[n+1])
let row=triangle.length
//倒数第一行初始化
let dp=new Array(triangle[row-1].length).fill(0).map((_,index)=>{
return triangle[row-1][index]
})
for(let i=row-2;i>=0;i--){ //倒数第一行已经被初始化了，这里从倒数第二行开始遍历
for(let j=0;j<triangle[i].length;j++){
dp[j]=Math.min(dp[j],dp[j+1])+triangle[i][j]
}
}
return dp[0]
};乘积最大子数组（存疑）
这个的特殊点在于，数组元素可以为负值。两个负值乘积就成了正数，这个题存储最小值就是这个原因
dp[n]的含义：最后一位的索引是n连续子数组的最大值、最小值、当前值
js
var maxProduct = function(nums) {
let dp=new Array(nums.length).fill(0).map((_,index)=>{
return {
min:nums[index],
max:nums[index],
cur:nums[index]
}
})
for(let i=1;i<nums.length;i++){
let curValue=dp[i].cur //其实也可以不在dp中存当前值,直接 let curValue=nums[i]
dp[i].max=Math.max(curValue,curValue*dp[i-1].min,curValue*dp[i-1].max)
dp[i].min=Math.min(curValue,curValue*dp[i-1].min,curValue*dp[i-1].max)
}
//dp数组中存储了所有最小值、最大值，这里是遍历取最大值
return dp.reduce((preItem,curItem)=>{
return curItem.max>preItem.max?curItem:preItem
}).max
};压缩dp数组，使用2个变量保存状态
有疑问
leetcode运行显示代码输出的是72，但实际上我本地运行就是正确答案12，暂时不清楚原因，记录下
js
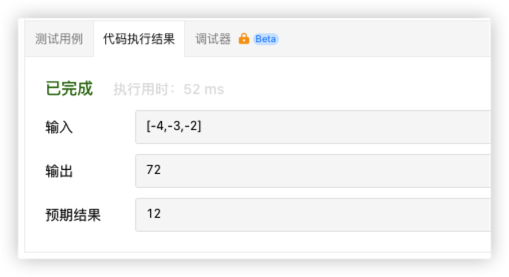
var maxProduct = function(nums) {
let preMax=nums[0]
let preMin=nums[0]
let res=nums[0]
for(let i=1;i<nums.length;i++){
let curValue=nums[i]
preMax=Math.max(curValue,curValue*preMax,curValue*preMin)
preMin=Math.min(curValue,curValue*preMax,curValue*preMin)
res=Math.max(preMax,res)
}
return res
};零钱兑换
js
var coinChange = function(coins, amount) {
//dp[0]本身无意义，但是如果amount=10，coins=[10]，coins刚好有一个10，下面的循环中dp[i-coinItem]+1就能保证是1
let dp=new Array(amount+1).fill(Infinity)
dp[0]=0
for(let i=1;i<=amount;i++){
for(coinItem of coins){
if(parseInt(coinItem)<=i){
dp[i]=Math.min(dp[i],dp[i-coinItem]+1)
}
}
}
return dp[amount]===Infinity?-1:dp[amount]
};贪心算法
122. 买卖股票的最佳时机 II
js
var maxProfit = function(prices){
let maxProfit=0
for(let i=1;i<prices.length;i++){
maxProfit=maxProfit+Math.max(0,prices[i]-prices[i-1])
}
return maxProfit
};有动态规划解法
455. 分发饼干
优先用尺寸大的饼干，来满足大胃口的孩子
js
var findContentChildren = function(g, s) {
//从小到大
g=g.sort((a,b)=>a-b)
s=s.sort((a,b)=>a-b)
//
let j=s.length-1
let res=0
for(let i=g.length;i>=0;i--){
if(s[j]>=g[i]&&j>=0){
res++
j--
}
}
return res
};435. 无重叠区间
只考虑右端是否能和下一个元素的左端重叠，不重叠就更新最新的右侧端点，并计数1次，表示无重叠区间个数
js
var eraseOverlapIntervals = function(intervals) {
//根据每个区间右侧端点元素，从小到大
intervals=intervals.sort((a,b)=>a[1]-b[1])
let right=intervals[0][1]
let res=1 //不重叠的区间个数
for(let i=1;i<intervals.length;i++){
if(right<=intervals[i][0]){ //无重叠
right=intervals[i][1]
res++
}
}
return intervals.length-res
};有动态规划解法
55. 跳跃游戏
动态规划解法
dp[i]表示：索引为i的位置是否可达的
js
var canJump = function(nums) {
let dp=new Array(nums.length).fill(false)
dp[0]=true //只有一个值得时候一定是可达的
for(let i=0;i<nums.length;i++){
for(let j=0;j<i;j++){
if(dp[j]===true&&j+nums[j]>=i){
dp[i]=true
break
}
}
}
return dp[nums.length-1]
};贪心解法
只考虑每个分段，合成的区间是否能覆盖到全部
js
var canJump = function(nums) {
let right=0
for(let i=0;i<nums.length;i++){
if(right>=i){ //只有最右侧索引覆盖到num[i]，才表示num[i]是可达的，否则这里都到不了
right=Math.max(nums[i]+i,right)
}
}
return right>=nums.length-1 //能覆盖的右侧索引>=数组最大索引，才能跳到最后一位
};881. 救生艇
按体重从小到大排序(题目显示所以人体重小于等于limit)
- 体重最大的 = limit ，则他自己乘坐一艘船
- 体重最大的 < limit ， 体重最小的+体重最大的<=limit则两人乘坐一艘船
JS
var numRescueBoats = function(people, limit) {
people=people.sort((a,b)=>{
return a-b
})
let left=0
let right=people.length-1
let res=0
while(left<=right){
if(people[left]+people[right]>limit&&people[right]<=limit){
right--
res++
}else if(people[left]+people[right]<=limit){
left++
right--
res++
}
}
return res
};452. 用最少数量的箭引爆气球
这个题和leetcode题号435思路一样，基本上就是确定重叠区间
这种情况可以考虑下，是需要两只箭的
js
var findMinArrowShots = function(points) {
points=points.sort((a,b)=>a[1]-b[1])
let right=points[0][1]
let resCount =1
for(let i=1;i<points.length;i++){
if(right<points[i][0]){ //不重叠
resCount++
right=points[i][1]
}
}
return resCount
};134. 加油站（跳过）
二分查找
二分查找要求数据必须有序
模版:
js
function xx(arr,target){
// 这里需要包含等于。即 left=right时，需要判断是否就是target
while(left<=right){
// 向下取整。
// 偶数个元素：[3,4]。(0+1)/2=0 （中间两个元素中的前一个元素）
// 奇数个元素：[3,4,5]。(0+2)/2=1 （中间元素）
const mid=Math.floor((left+right)/2)
if(arr[mid]===target){
return 结果
}else if(arr[mid]<target){
left=mid+1
} else{
right=mid-1
}
}
return 没找到，输出
// 注意：
// 无论元素个数是奇还是偶，都会走到left===right的情况
// 情况1：如果arr[mid]===target，最终结果===> mid位置就是所在位置
// 情况2：如果不等于，那么mid在 left===right 的位置，right、left有一个位置会变化。注意mid的值可能溢出数组了，例如arr=[1],target=2。最终结果===> 由while外部的return输出
// 2-1 arr[mid]<target , left后移一位
// 2-2 target<arr[mid] , right前移一位
// 最后一轮 left===right ，(target)表示
mid=l=r
|
x y z
// arr[mid]!==target的情况也很有价值（35、69题），数组中没有target了，下面（target）表示其应该防止的位置
// 2-1
mid=r l
| |
x y (target) z
// 2-2
r mid=l
| |
x (target) y z
// 总结最后一轮： target左侧是r，右侧是l
}704. 二分查找
题目
js
//给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否
//则返回 -1。二分法：
js
var binarySearch = function(nums, target) {
let left=0,right=nums.length-1
while(left<=right){
const mid=Math.floor((left+right)/2)
if(nums[mid]===target){
return mid
}else if(nums[mid]<target){
left=mid+1
}else {
right=mid-1
}
}
return -1
};35. 搜索插入位置
题目
js
//给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
//
// 请必须使用时间复杂度为 O(log n) 的算法二分法
js
var searchInsert = function(nums, target) {
let left=0,right=nums.length-1
let mid=0
while (left<=right){
mid=Math.floor((left+right)/2)
if (nums[mid]===target) {
return mid
}else {
if (nums[mid]<target){
left=mid+1
}else {
right=mid-1
}
}
}
return left
};69. x 的平方根
题目
js
//给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
//
// 由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。
//
// 注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。
//
//
//
// 示例 1：
//
//
//输入：x = 4
//输出：2
//
//
// 示例 2：
//
//
//输入：x = 8
//输出：2
//解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。
//
//
//
//
// 提示：
//
//
// 0 <= x <= 2³¹ - 1
//
//
// Related Topics 数学 二分查找 👍 1511 👎 0二分法
js
var mySqrt = function(x) {
//x=0
let left=1,right=x
// mid*mid===x mid
// mid*mid<x mid
// mid*mid>x mid-1
while (left<=right){
const mid=Math.floor((left+right)/2)
if(mid*mid===x){
return mid
}else if (mid*mid<x){
left= mid+1
}else {
right=mid-1
}
}
// x就相当于target ， 最后一轮一定是：right target left
// 返回right是因为返回的平方根要取整
return right
};300. 最长递增子序列
题目
js
//给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
//
// 子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子
//序列。
//
// 示例 1：
//
//
//输入：nums = [10,9,2,5,3,7,101,18]
//输出：4
//解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
//
//
// 示例 2：
//
//
//输入：nums = [0,1,0,3,2,3]
//输出：4
//
//
// 示例 3：
//
//
//输入：nums = [7,7,7,7,7,7,7]
//输出：1
//
//
//
//
// 提示：
//
//
// 1 <= nums.length <= 2500
// -10⁴ <= nums[i] <= 10⁴
//
//
//
//
// 进阶：
//
//
// 你能将算法的时间复杂度降低到 O(n log(n)) 吗?
//
//
// Related Topics 数组 二分查找 动态规划 👍 3567 👎 0动态规划
js
var lengthOfLIS = function(nums) {
// dp[i] : 0-i元素中最长递增子序列值
let dp=new Array(nums.length).fill(1)
for (let i=1;i<nums.length;i++){
for (let j = 0; j < i; j++) {
// 一直在更新dp[i]
if (nums[j]<nums[i]){
dp[i]=Math.max(dp[i],dp[j]+1)
}
}
}
return Math.max(...dp)
};二分+贪心
这种方式可以求出最长递增子序列是什么，动态规划只能求出来结果的长度
js
var lengthOfLIS = function(nums) {
// 35题，left就是最终插入的位置
function getInsertIndex(arr,target){
let left=0,right=arr.length-1
while (left<=right){
const mid=Math.floor((left+right)/2)
if(arr[mid]===target){
return mid
}else if(arr[mid]<target){
left=mid+1
}else {
right=mid-1
}
}
return left // right target left
}
if (nums.length===0){
return 0
}
let resArr=[nums[0]]
for (let i=1;i<nums.length;i++){
if(nums[i]>resArr[resArr.length-1]){
// 追加到末尾
resArr.push(nums[i])
}else{
// 二分插入
const index=getInsertIndex(resArr,nums[i])
// 覆盖 right (target) left，target插入的是left的位置，所以数组中left被替换为更小的值target。（贪心，换的更小，更有机会组成最长的子序列）
resArr[index]=nums[i]
}
}
return resArr.length
};4. 寻找两个正序数组的中位数
题目
js
//给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
//
// 算法的时间复杂度应该为 O(log (m+n)) 。
//
//
//
// 示例 1：
//
//
//输入：nums1 = [1,3], nums2 = [2]
//输出：2.00000
//解释：合并数组 = [1,2,3] ，中位数 2
//
//
// 示例 2：
//
//
//输入：nums1 = [1,2], nums2 = [3,4]
//输出：2.50000
//解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
//
//
//
//
//
//
// 提示：
//
//
// nums1.length == m
// nums2.length == n
// 0 <= m <= 1000
// 0 <= n <= 1000
// 1 <= m + n <= 2000
// -10⁶ <= nums1[i], nums2[i] <= 10⁶
//
//
// Related Topics 数组 二分查找 分治 👍 7017 👎 0二分
js
var findMedianSortedArrays = function(nums1, nums2) {
const len1=nums1.length
const len2=nums2.length
let ptr1=0,ptr2=0
let composeList=[]
// 合并
while (ptr1<=len1-1&&ptr2<=len2-1){
if(nums1[ptr1]<=nums2[ptr2]){
composeList.push(nums1[ptr1])
ptr1++
}else {
composeList.push(nums2[ptr2])
ptr2++
}
}
if (ptr1<=len1-1){
composeList.push(...nums1.slice(ptr1))
}else {
composeList.push(...nums2.slice(ptr2))
}
// 算中位数
const mid=Math.floor((composeList.length-1)/2)//mid计算工时，注意left索引，right索引加和后除以2向下取整,算出来的mid是中间数字的`索引`
if (composeList.length%2===0){
return (composeList[mid]+composeList[mid+1])/2
}else {
return composeList[mid]
}
};162. 寻找峰值
题目
js
//峰值元素是指其值严格大于左右相邻值的元素。
//
// 给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。
//
// 你可以假设 nums[-1] = nums[n] = -∞ 。
//
// 你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
//
//
//
// 示例 1：
//
//
//输入：nums = [1,2,3,1]
//输出：2
//解释：3 是峰值元素，你的函数应该返回其索引 2。
//
// 示例 2：
//
//
//输入：nums = [1,2,1,3,5,6,4]
//输出：1 或 5
//解释：你的函数可以返回索引 1，其峰值元素为 2；
// 或者返回索引 5， 其峰值元素为 6。
//
//
//
//
// 提示：
//
//
// 1 <= nums.length <= 1000
// -2³¹ <= nums[i] <= 2³¹ - 1
// 对于所有有效的 i 都有 nums[i] != nums[i + 1]
//
//
// Related Topics 数组 二分查找 👍 1259 👎 0暴力模拟
js
var findPeakElement = function(nums) {
if(nums.length===1){
return 0
}
nums.push(-Infinity)
nums.unshift(-Infinity)
let left=0,right=1
while(right<nums.length){
if( nums[left] < nums[right]){
left++
right++
// 最后一个元素使无穷小，这个一定能命中
if(nums[left] > nums[right]){
return left-1 // 因为数组在开头补了一个负无穷，这里需要-1
}
}else {
left++
right++
}
}
};二分法 题解
js
var findPeakElement = function(nums) {
nums.push(-Infinity)
nums.unshift(-Infinity)
let left=0,rigth=nums.length-1
while (left<=rigth){
const mid=Math.floor((left+rigth)/2)
if(nums[mid-1]<nums[mid]&&nums[mid]>nums[mid+1]){
return mid-1 // 数组开头补了一个负无穷
}else if(nums[mid-1]>nums[mid]){
rigth=mid-1
}else {
left=mid+1
}
}
// 代码一定不会走到这里。
// 题目限制了：对于所有有效的 i 都有 nums[i] != nums[i + 1] 和 假设 nums[-1] = nums[n] = -∞ 。
};找最大值，其两侧一定是小于最大值的
js
var findPeakElement = function(nums) {
let maxIdex=0
for(let i=0;i<nums.length;i++){
if(nums[i]>nums[maxIdex]){
maxIdex=i
}
}
return maxIdex
};74. 搜索二维矩阵
题目
js
//给你一个满足下述两条属性的 m x n 整数矩阵：
//
//
// 每行中的整数从左到右按非严格递增顺序排列。
// 每行的第一个整数大于前一行的最后一个整数。
//
//
// 给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。
//
//
//
// 示例 1：
//
//
//输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
//输出：true
//
//
// 示例 2：
//
//
//输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
//输出：false
//
//
//
//
// 提示：
//
//
// m == matrix.length
// n == matrix[i].length
// 1 <= m, n <= 100
// -10⁴ <= matrix[i][j], target <= 10⁴
//
//
// Related Topics 数组 二分查找 矩阵 👍 901 👎 0二分法
js
var searchMatrix = function(matrix, target) {
function searchIndex(nums,target){
let left=0,right=nums.length-1
while (left<=right){
const mid=Math.floor((left+right)/2)
if(nums[mid]===target){
return {index:mid,status:true}
}else if (nums[mid]<target){
left=mid+1
}else {
right=mid-1
}
}
return {index:right,status:false}
}
// 先用二分法确定在哪行
let firstList=[]
for (let row of matrix){
firstList.push(row[0])
}
const {index,status}=searchIndex(firstList,target)
if (status){
return true
}else if (index<firstList.length&&index>=0){
return searchIndex(matrix[index],target).status
}else {
return false
}
};34. 在排序数组中查找元素的第一个和最后一个位置
题目
js
//给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
//
// 如果数组中不存在目标值 target，返回 [-1, -1]。
//
// 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
//
//
//
// 示例 1：
//
//
//输入：nums = [5,7,7,8,8,10], target = 8
//输出：[3,4]
//
// 示例 2：
//
//
//输入：nums = [5,7,7,8,8,10], target = 6
//输出：[-1,-1]
//
// 示例 3：
//
//
//输入：nums = [], target = 0
//输出：[-1,-1]
//
//
//
// 提示：
//
//
// 0 <= nums.length <= 10⁵
// -10⁹ <= nums[i] <= 10⁹
// nums 是一个非递减数组
// -10⁹ <= target <= 10⁹
//
//
// Related Topics 数组 二分查找 👍 2630 👎 0二分
js
var searchRange = function(nums, target) {
function search(nums,target){
let left=0,right=nums.length
while (left<=right){
const mid=Math.floor((left+right)/2)
if (target===nums[mid]){
return {status:true,index: mid}
}else if(target<nums[mid]){
right=mid-1
}else {
left=mid+1
}
}
return {status:false,index: -1}
}
const {status,index}=search(nums,target)
if (status){
let rightOffset=index
while (nums[rightOffset]===nums[rightOffset+1]){
rightOffset++
}
let leftOffset=index
while (nums[leftOffset]===nums[leftOffset-1]){
leftOffset--
}
return [leftOffset,rightOffset]
}else {
return [-1,-1]
}
};153. 寻找旋转排序数组中的最小值
题目
js
//给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
//
// 如果数组中不存在目标值 target，返回 [-1, -1]。
//
// 你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
//
//
//
// 示例 1：
//
//
//输入：nums = [5,7,7,8,8,10], target = 8
//输出：[3,4]
//
// 示例 2：
//
//
//输入：nums = [5,7,7,8,8,10], target = 6
//输出：[-1,-1]
//
// 示例 3：
//
//
//输入：nums = [], target = 0
//输出：[-1,-1]
//
//
//
// 提示：
//
//
// 0 <= nums.length <= 10⁵
// -10⁹ <= nums[i] <= 10⁹
// nums 是一个非递减数组
// -10⁹ <= target <= 10⁹
//
//
// Related Topics 数组 二分查找 👍 2630 👎 0排序
js
var findMin = function(nums) {
return nums.sort((a,b)=>a-b)[0]
};二分
旋转后的图
js
// [a[n-1], a[0], a[1], a[2], ..., a[n-2]]
// 最小值a[0]小于左侧、右侧，且只有他一个值符合这种条件
var findMin = function(nums) {
let left=0,right=nums.length-1
// 这里没有使用<=。像这种收缩区间的逻辑，最后必然会有left===right的情况
// 二分查找是while (left<=right)，是因为需要再 left===right验证下结果是否是target
// 这里left<right时循环，循环结束时left===right，直接输出了 nums[left]或nums[right]
while (left<right){
const mid=Math.floor((left+right)/2)
// 题目有元素值互不相同的要求，所以没有等于的情况
if(nums[mid]<nums[right]){
right=mid
}else if (nums[mid]>nums[right]) {
left=mid+1
}
}
return nums[left]
};374. 猜数字大小
题目
js
//猜数字游戏的规则如下：
//
//
// 每轮游戏，我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。
// 如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。
//
//
// 你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有 3 种可能的情况（-1，1 或 0）：
//
//
// -1：我选出的数字比你猜的数字小 pick < num
// 1：我选出的数字比你猜的数字大 pick > num
// 0：我选出的数字和你猜的数字一样。恭喜！你猜对了！pick == num
//
//
// 返回我选出的数字。
//
//
//
// 示例 1：
//
//
//输入：n = 10, pick = 6
//输出：6
//
//
// 示例 2：
//
//
//输入：n = 1, pick = 1
//输出：1
//
//
// 示例 3：
//
//
//输入：n = 2, pick = 1
//输出：1
//
//
// 示例 4：
//
//
//输入：n = 2, pick = 2
//输出：2
//
//
//
//
// 提示：
//
//
// 1 <= n <= 2³¹ - 1
// 1 <= pick <= n
//
//
// Related Topics 二分查找 交互 👍 336 👎 0二分
js
var guessNumber = function(n) {
let left=1,right=n
while (left<=right){
const mid=Math.floor((left+right)/2)
const res=guess(mid)
if (res===0){
return mid
}else if (res===1){
left=mid+1
}else {
right=mid-1
}
}
// 挑选的值一定在 1-n之间，代码不会走到这里
};总结
while(left<right)
162、153都是通过二分收缩区间，最后返回left===right的那个值，不必再进行if判断了
while(left<=right)
其他题都是，在二分区间找target值，需要left===right时对比下是否是target双指针
类型
- 对撞指针：两个指针向中间收紧（二分法也是）
- 普通指针：两个指针同向、背向移动
- 快慢指针：两个指针一快一慢
总结（参考这里）
链表的两个劣势：无法高效获取长度，无法根据偏移快速访问元素
但是面试的时候经常碰见取倒数第k个元素，获取中间位置的元素，判断链表是否存在环，判断环的长度等和长度与位置有关的问题。这些问题都可以双指针来解决
倒数第k个元素的问题
初始：设有两个指针 p 和 q，初始时均指向头结点 步骤： 1、先让 p 沿着 next 移动 k 次。此时，p 指向第 k+1个结点，q 指向头节点，两个指针的距离为 k 2、同时移动 p 和 q，直到 p 指向空，此时 q 即指向倒数第 k 个结点获取中间元素的问题
js初始：设有两个指针 fast 和 slow，初始时指向头节点。 步骤： 每次移动时，fast向后走两次，slow向后走一次，直到 fast 无法向后走两次。这使得在每轮移动之后。fast 和 slow 的距离就会增加1 （设链表有 n 个元素，那么最多移动 n/2 轮。 当 n 为奇数时，slow 恰好指向中间结点 当 n 为 偶数时，slow 恰好指向中间两个结点的前一个还是后一个，和判断条件相关。876题要求返回靠后的一个 ）偶数个
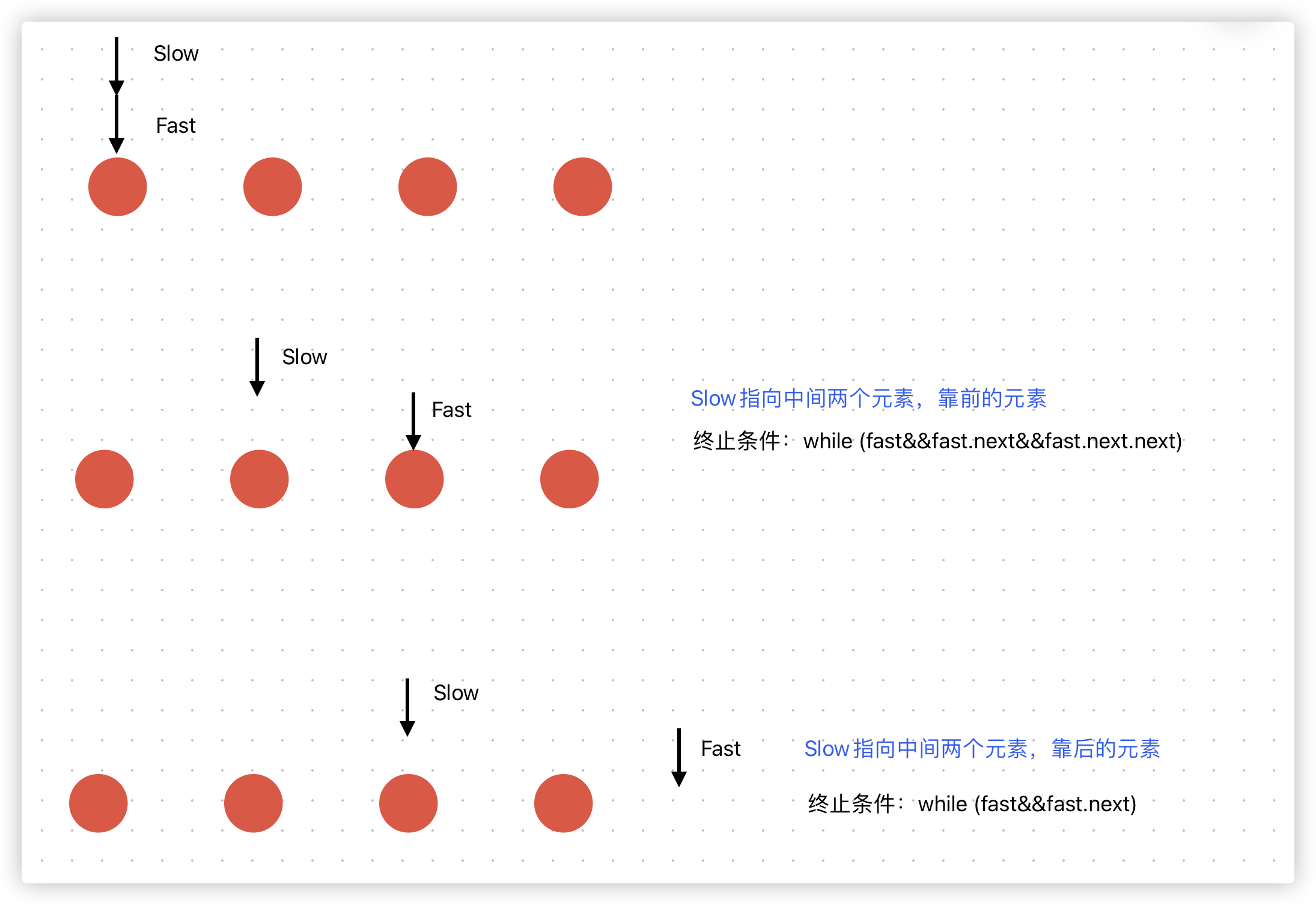
奇数个
是否存在环问题
初始：设有两个指针 fast 和 slow，初始时指向头节点。 步骤： 每次移动时，fast向后走两次，slow向后走一次，直到 fast 无法向后走两次。这使得在每轮移动之后。fast 和 slow 的距离就会增加1 (这就变成了追及相遇问题，一旦进入环中循环，快的总会追上慢的)如果存在环，如何判断环的长度
快慢指针相遇后继续移动，直到第二次相遇。两次相遇间的移动次数即为环的长度。
26. 删除有序数组中的重复项
题目要求原地，即空间复杂度为 O(1)
对于数组这种结构，原地大多意味着覆盖、交换
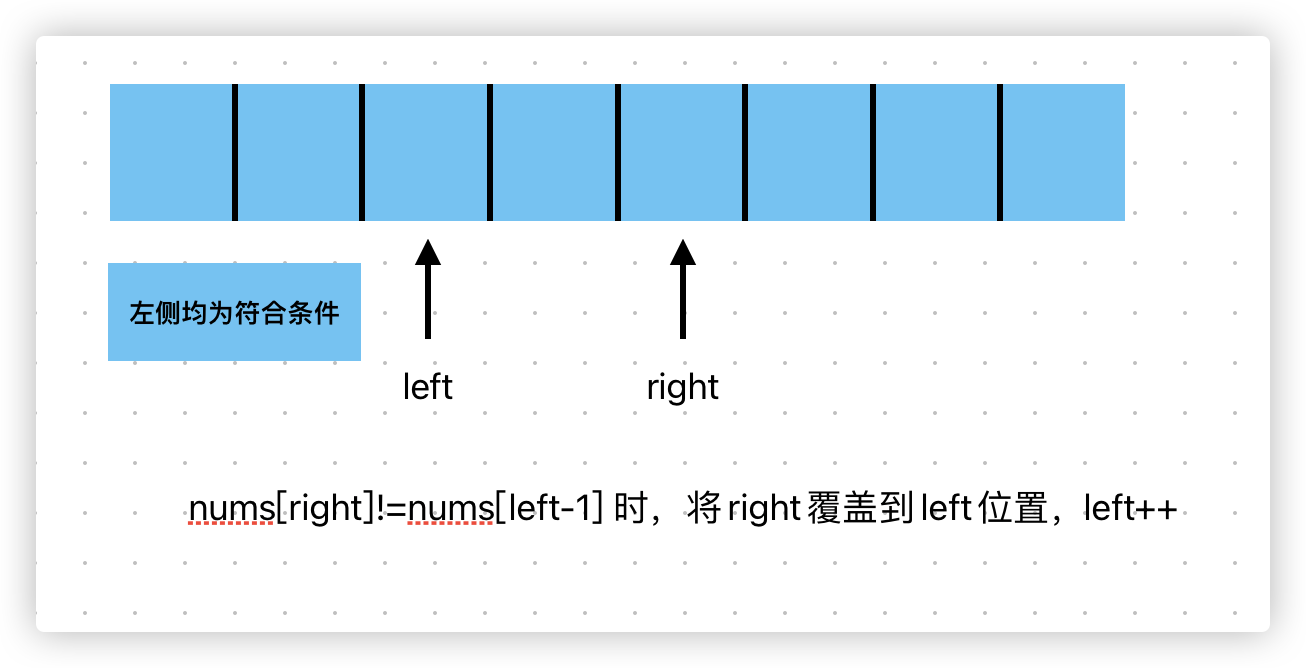
通过交换两个指针元素，left左侧（不包括left）是符合条件的元素，right查找符合条件的元素覆盖left的位置，之后left++
ts
var removeDuplicates = function(nums) {
const len=nums.length
let left=right=1 // 注意这里空出来一个left左侧留一个元素。这个题目要求数组长度>=1，所以不怕越界
for (;right<len;right++){
if(nums[left-1]!==nums[right]){// right是扫描剩下所有内容的，索引是right。left-1才是符合条件的元素，left留出了1个单位的缓冲区。未来符合条件的right元素都是覆盖到这个缓冲区里的
nums[left]=nums[right]
left++
}
}
return left
};80. 删除有序数组中的重复项 II
js
var removeDuplicates = function(nums) {
// 快慢指针
const len=nums.length
if (len<2){
return len
}
let left=right=2
for (;right<len;right++){
// 1 1 1
if (nums[left-2]!==nums[right]){
nums[left]=nums[right]
left++
}
}
return left
};141. 环形链表
题目
js
//给你一个链表的头节点 head ，判断链表中是否有环。
//
// 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到
//链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
//
// 如果链表中存在环 ，则返回 true 。 否则，返回 false 。
//
//
//
// 示例 1：
//
//
//
//
//输入：head = [3,2,0,-4], pos = 1
//输出：true
//解释：链表中有一个环，其尾部连接到第二个节点。
//
//
// 示例 2：
//
//
//
//
//输入：head = [1,2], pos = 0
//输出：true
//解释：链表中有一个环，其尾部连接到第一个节点。
//
//
// 示例 3：
//
//
//
//
//输入：head = [1], pos = -1
//输出：false
//解释：链表中没有环。
//
//
//
//
// 提示：
//
//
// 链表中节点的数目范围是 [0, 10⁴]
// -10⁵ <= Node.val <= 10⁵
// pos 为 -1 或者链表中的一个 有效索引 。
//
//
//
//
// 进阶：你能用 O(1)（即，常量）内存解决此问题吗？
//
// Related Topics 哈希表 链表 双指针 👍 2113 👎 0天秀解法：题解地址 ，leetcode上看到了很有意思的三种解法，这三种解法都是因为js的特性
js
var hasCycle = function(head) {
while(head!==null){
if(!head.tag){
head.tag=true // 没有标记的节点，增加一个标记
head=head.next
}else{
return true
}
}
return false
};哈希记录节点
js
var hasCycle = function(head) {
let m=new Map()
while(head!==null){
if(!m.has(head)){
m.set(head,1) // 存的是节点的引用
head=head.next
}else{
return true
}
}
return false
};快慢指针
js
var hasCycle = function(head) {
let fast=head,slow=head
// 之所以有fast.next这个条件，可以想下[1] 这个例子
while (fast&&fast.next){
fast=fast.next.next
slow=slow.next
if(fast===slow){
return true
}
}
return false
};142. 环形链表 II
题目
js
//给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
//
// 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到
//链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
//
// 不允许修改 链表。
//
//
//
//
//
//
// 示例 1：
//
//
//
//
//输入：head = [3,2,0,-4], pos = 1
//输出：返回索引为 1 的链表节点
//解释：链表中有一个环，其尾部连接到第二个节点。
//
//
// 示例 2：
//
//
//
//
//输入：head = [1,2], pos = 0
//输出：返回索引为 0 的链表节点
//解释：链表中有一个环，其尾部连接到第一个节点。
//
//
// 示例 3：
//
//
//
//
//输入：head = [1], pos = -1
//输出：返回 null
//解释：链表中没有环。
//
//
//
//
// 提示：
//
//
// 链表中节点的数目范围在范围 [0, 10⁴] 内
// -10⁵ <= Node.val <= 10⁵
// pos 的值为 -1 或者链表中的一个有效索引
//
//
//
//
// 进阶：你是否可以使用 O(1) 空间解决此题？
//
// Related Topics 哈希表 链表 双指针 👍 2479 👎 0哈希记录节点
js
var detectCycle = function(head) {
let m=new Map()
while(head){
if(m.has(head)){
return head
}else {
m.set(head,true)
head=head.next
}
}
return null
};快慢指针(略)
15. 三数之和
数组从小到大排序。
使用i、L、R三个指针
- i 从头遍历
- L=i+1
- R=len-1
L到R框选了剩余的数字集合
- L+R>-i ，那就缩小一点，即R=R-1
- L+R<-i ，那就放大一点，即L=L+1
- L+R=-i ，就加入结果集合
还有就是三元组不能重复，所以还要有一些判重逻辑
js
var threeSum = function(nums) {
let res=[]
nums.sort((a,b)=>a-b)
for (let i=0;i<nums.length;i++){
// 防止重复
if(i>0&&nums[i]===nums[i-1]){
continue
}
// i指针数字>0，数组从小到大排序的，所以加上L、R肯定不等于0
if (nums[i]>0){
return res
}
let L=i+1,R=nums.length-1
while (L<R){
if(nums[i]+nums[L]+nums[R]===0){
res.push([nums[i],nums[L],nums[R]])
// 必须要过滤一下
// 例如：[-1,0,0,1,1] ，res=[-1,0,1],这时候就不能让L继续为0，R继续为1
let historyValue=nums[R]
while (historyValue===nums[R]&&L<R){
R--
}
historyValue=nums[L]
while (historyValue===nums[L]&&L<R){
L++
}
}else if(nums[i]+nums[L]+nums[R]>0){
R--
}else {
L++
}
}
}
return res
};11. 盛最多水的容器
容量取决于最小高度的边，尝试移动最小边是否会获得更大的容量
js
var maxArea = function(height) {
let left=0,right=height.length-1
let maxCapcity=0
while (left<right){
maxCapcity=Math.max((right-left)*Math.min(height[left],height[right]),maxCapcity)
if (height[left]<height[right]){
left++
}else {
right--
}
}
return maxCapcity
};160. 相交链表
哈希计数：把链表A路过的节点存下，在遍历链表B，查找是否存在
js
var getIntersectionNode = function(headA, headB) {
let m=new Map()
while (headA){
if (!m.has(headA)){
m.set(headA,true)
}
headA=headA.next
}
while (headB){
if (m.has(headB)){
return headB
}
headB=headB.next
}
return null
};双指针
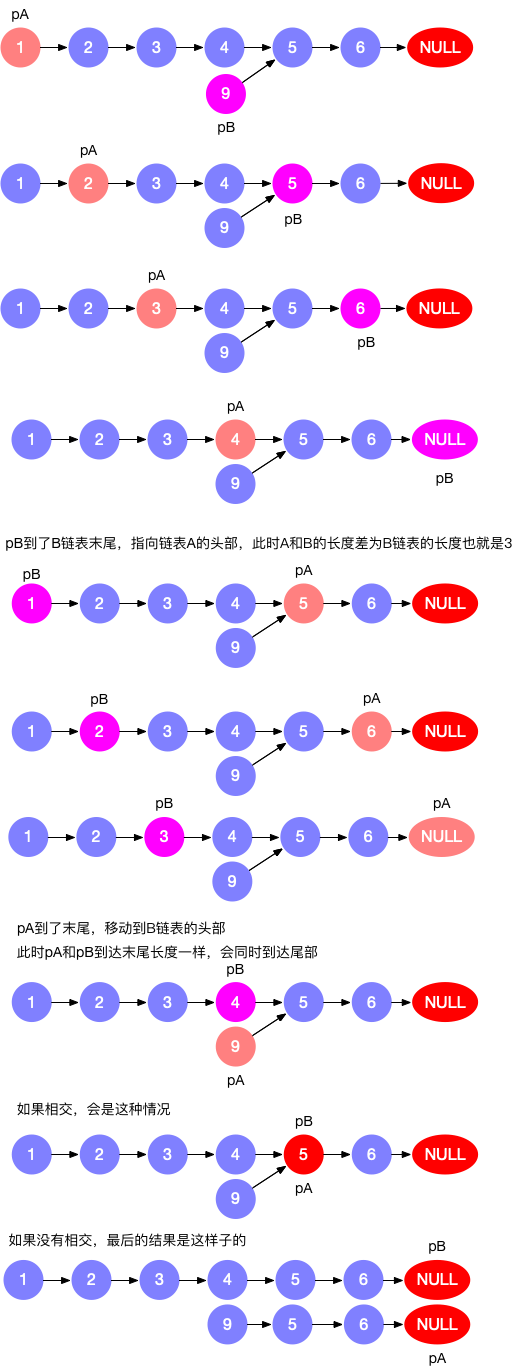
A、B两个链表长度不一样，只有当A节点走完自己的再走B的，B节点走完自己的再走A的，才能保证他们会出现相交。如何走到最后都没有相交就是不相交
js
var getIntersectionNode = function(headA, headB) {
let A=headA,B=headB
// 如果链表不相交，最后headA=headB=null，也会结束循环
while (headA!==headB){
if (headA){
headA=headA.next
}else {
headA=B
}
if (headB){
headB=headB.next
}else {
headB=A
}
}
return headA
};876. 链表的中间结点
题目
js
//给你单链表的头结点 head ，请你找出并返回链表的中间结点。
//
// 如果有两个中间结点，则返回第二个中间结点。
//
//
//
// 示例 1：
//
//
//输入：head = [1,2,3,4,5]
//输出：[3,4,5]
//解释：链表只有一个中间结点，值为 3 。
//
//
// 示例 2：
//
//
//输入：head = [1,2,3,4,5,6]
//输出：[4,5,6]
//解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。
//
//
//
//
// 提示：
//
//
// 链表的结点数范围是 [1, 100]
// 1 <= Node.val <= 100
//
//
// Related Topics 链表 双指针 👍 975 👎 0双指针（注意如果节点个数是偶数个，这题要求返回的是中间两个节点中，靠后的一个）
js
var middleNode = function(head) {
let left=head,right=head
while (right&&right.next){
left=left.next
right=right.next.next
}
return left
};滑动窗口
滑动窗口 ，使用左右指针限制窗口大小
for循环移动right指针时
每轮for循环实际上right都右移了，加入窗口
每轮都判断left是否需要收缩窗口
set、hash集合始终记录窗口内的数据(操作窗口时，记得维护set、hash数据)
题目特征：连续的，求最值
3. 无重复字符的最长子串
滑动窗口，因为要求不重复，所以采用set来实时记录窗口内数据
注意：这个题描述的不准确，应该是连续子串。连续子串才能用滑动窗口
从这个题我发现滑动窗口的一个细节点：
- right放入窗口前，一直维护窗口，符合条件后再将right放入。这个题属于这种
- right放入窗口后，再一直维护窗口直到符合条件
js
var lengthOfLongestSubstring = function(s) {
// 记录滑动窗口数据。可以快速判断 right指针添加的元素是否在窗口中存在，如果存在就移动left剔除
let winRecordSet=new Set()
let maxLen=0
let left=0,right=0
for(;right<s.length;right++){
if(winRecordSet.has(s[right])){
// 准备新加的元素在窗口内存在重复，通过左端点++，缩小窗口维护窗口内不重复的条件成立
while(winRecordSet.has(s[right])){
winRecordSet.delete(s[left])
left++
}
// 重复的元素剔除了，在把right放进去
winRecordSet.add(s[right])
}else{
// 新加元素，在窗口不存在重复
winRecordSet.add(s[right])
}
maxLen=Math.max(maxLen,winRecordSet.size)
}
return maxLen
};53. 最大子数组和
下面递归里有这个题
219. 存在重复元素 II
题目
js
//给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i
//- j) <= k 。如果存在，返回 true ；否则，返回 false 。滑动窗口
js
var containsNearbyDuplicate = function(nums, k) {
// 一个元素
if (nums.length===1){
return false
}
// 大于1个元素
let s=new Set()
let left=0,right=1
s.add(nums[0])
for (;right<nums.length;right++){
// 不管if是否为true，实际上每一轮right都移动了
if (right-left<=k){
if (s.has(nums[right])){
return true
}
s.add(nums[right])
}else {
s.delete(nums[left])
left++
// 同if中的逻辑
if (s.has(nums[right])){
return true
}
s.add(nums[right])
}
}
return false
};提出共同逻辑，简化下
js
var containsNearbyDuplicate = function(nums, k) {
// 一个元素
if (nums.length===1){
return false
}
// 大于1个元素
let s=new Set()
let left=0,right=1
s.add(nums[0])
for (;right<nums.length;right++){
// 如果本次右移超过了窗口最大值，立即收紧left
// 这个必须写在前面，因为这里不收紧left，下面的if判断区间的大小就不在 k 之间了
if (right-left>k){
s.delete(nums[left])
left++
}
// 每次right右移都做的逻辑
if (s.has(nums[right])){
return true
}
s.add(nums[right])
}
return false
};438.找到字符串中所有字母异位词
滑动窗口中可能出现重复字符，不能使用Set存储。我们使用Hash计数存储
为了判断 窗口中的字符与p是否为异位词，我们把p也转换为哈希存储，这样就可以对比了
js
var findAnagrams = function(s, p) {
function isSetIncludeStr(winHash,needHash){
for(let key of Object.keys(needHash)){
if(winHash[key]!==needHash[key]){
return false
}
}
return true
}
if (s.length<p.length){
return []
}
// 把p转成哈希（这是因为窗口也是哈希，便于比较两者是否包含相同且数量一致的字符）
let needHash={}
for (let val of p){
if(!needHash[val]){
needHash[val]=0
}
needHash[val]++
}
// 窗口宽度 起始
let left=0,right=0
// 窗口内容
let winHash={}
// 结果
let res=[]
for (;right<s.length;right++){
// 记录窗口内部的数据
if(!winHash[s[right]]){
winHash[s[right]]=0
}
winHash[s[right]]++
// 维护滑动窗口宽度。这里用if执行一次，就可以维护好窗口
// 904题用while需要循环才能维护好
if (right-left+1>p.length){
winHash[s[left]]--
left++
}
//---- 一般题目都是这里处理逻辑 -----
// 这个题窗口宽度是p.length是才可能是异位词。
if (right-left+1===p.length){
// 判断是否为异位词
if (isSetIncludeStr(winHash,needHash)){
res.push(left)
}
}
}
return res
};1456. 定长子串中元音的最大数目
题目
js
//给你字符串 s 和整数 k 。
//
// 请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。
//
// 英文中的 元音字母 为（a, e, i, o, u）。
//
//
//
// 示例 1：
//
// 输入：s = "abciiidef", k = 3
//输出：3
//解释：子字符串 "iii" 包含 3 个元音字母。
//
//
// 示例 2：
//
// 输入：s = "aeiou", k = 2
//输出：2
//解释：任意长度为 2 的子字符串都包含 2 个元音字母。
//
//
// 示例 3：
//
// 输入：s = "leetcode", k = 3
//输出：2
//解释："lee"、"eet" 和 "ode" 都包含 2 个元音字母。
//
//
// 示例 4：
//
// 输入：s = "rhythms", k = 4
//输出：0
//解释：字符串 s 中不含任何元音字母。
//
//
// 示例 5：
//
// 输入：s = "tryhard", k = 4
//输出：1
//
//
//
//
// 提示：
//
//
// 1 <= s.length <= 10^5
// s 由小写英文字母组成
// 1 <= k <= s.length
//
//
// Related Topics 字符串 滑动窗口 👍 92 👎 0解
js
var maxVowels = function(s, k) {
let left=0,right=0
let winHash={}
let targetList= ['a','e','i','o','u']
let max=0
for (;right<s.length;right++){
// 记录窗口内部的数据
if (!winHash[s[right]]){
winHash[s[right]]=0
}
winHash[s[right]]++
// 维护滑动窗口宽度
if (right-left+1>k){
winHash[s[left]]--
left++
}
// 窗口宽度在这个区间内部，做逻辑处理
if (right-left+1>=k){
let temp=0
for (let val of targetList){
if(winHash[val]){
temp+=winHash[val]
}
}
max=Math.max(max,temp)
}
}
return max
};76. 最小覆盖子串
滑动窗口，left-right范围包含t，left收紧区间，一旦区间不再能包含t了，right放大区间
js
var minWindow = function(s, t) {
function isWinIncludeAllStr(winHash,needHash){
for (let val of Object.keys(needHash)){
if (!winHash[val]||winHash[val]<needHash[val]){
return false
}
}
return true
}
// 把t转行为哈希
let needHash={}
for (let val of t){
if(!needHash[val]){
needHash[val]=0
}
needHash[val]++
}
// 窗口
let left=0,right=0
let winHash={}
// 最小时，左右指针（初始值为最大的数）
let res=[0,Infinity]
for (;right<s.length;right++){
// 记录窗口内部的数据
if(!winHash[s[right]]){
winHash[s[right]]=0
}
winHash[s[right]]++
// 维护滑动窗口宽度
while(isWinIncludeAllStr(winHash,needHash)){
// 这题的逻辑判断，放在了调整窗口内部了
// 这是因为放在同级，还需要再调用下isWinIncludeAllStr，比较浪费
if(res[1]-res[0]>right-left){
res=[left,right]
}
winHash[s[left]]--
if(winHash[s[left]]===0){
delete winHash[s[left]] // 因为没有用到 Object.keys()。所以这里不清除也行
}
left++
}
}
if (res[1]-res[0]<Infinity){
return s.slice(res[0],res[1]+1)
}else {
return ''
}
};904. 水果成篮
题目
这个题好像出错了，题目要求返回最大的水果数，实际上应该是：取最大的水果数时，树的个数
js
//你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果 种类 。
//
// 你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：
//
//
// 你只有 两个 篮子，并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
// 你可以选择任意一棵树开始采摘，你必须从 每棵 树（包括开始采摘的树）上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到
//下一棵树，并继续采摘。
// 一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
//
//
// 给你一个整数数组 fruits ，返回你可以收集的水果的 最大 数目。
//
//
//
// 示例 1：
//
//
//输入：fruits = [1,2,1]
//输出：3
//解释：可以采摘全部 3 棵树。
//
//
// 示例 2：
//
//
//输入：fruits = [0,1,2,2]
//输出：3
//解释：可以采摘 [1,2,2] 这三棵树。
//如果从第一棵树开始采摘，则只能采摘 [0,1] 这两棵树。
//
//
// 示例 3：
//
//
//输入：fruits = [1,2,3,2,2]
//输出：4
//解释：可以采摘 [2,3,2,2] 这四棵树。
//如果从第一棵树开始采摘，则只能采摘 [1,2] 这两棵树。
//
//
// 示例 4：
//
//
//输入：fruits = [3,3,3,1,2,1,1,2,3,3,4]
//输出：5
//解释：可以采摘 [1,2,1,1,2] 这五棵树。
//
//
//
//
// 提示：
//
//
// 1 <= fruits.length <= 10⁵
// 0 <= fruits[i] < fruits.length
//
//
// Related Topics 数组 哈希表 滑动窗口 👍 626 👎 0解
js
var totalFruit = function(fruits) {
let left=0,right=0
let hash= {}
// 最大水果数
let fruitsMax=0
// 取得最大水果数时，用了几棵树
let treeNum=0
for (;right<fruits.length;right++){
if (!hash[fruits[right]]){
hash[fruits[right]]=0
}
hash[fruits[right]]++
// 维护窗口。 特别注意,hash存储的特点是：例如hash['a']=0，即使没有数据a了，仍然能遍历到这个值，所以推荐为0后，删除该key
while (Object.keys(hash).length>2){
hash[fruits[left]]--
if (hash[fruits[left]]===0){
delete hash[fruits[left]]
}
left++
}
// 逻辑处理
// 一开始写的 Object.keys(hash).length===2 ，一个数一定小于两个数，所以觉得最大值一定出在等于2的时候
// 用例 [0] ，即只有一个树的时候
if (Object.keys(hash).length<=2){
let temp=0
for (let count of Object.values(hash)){
temp+=count
}
if (temp>fruitsMax){
fruitsMax=temp
treeNum=right-left+1
}
}
}
return treeNum
};239. 滑动窗口最大值
滑动窗口暴力解法超时
js
// 经典模版
var maxSlidingWindow = function(nums, k) {
let res=[]
let left=right=0
// for 右指针 ， for循环会先把窗口扩大到k，然后触发while维护窗口
for (;right<nums.length;right++){
// while 维护滑动窗口。不断通过left++缩小窗口
while (right-left+1===k){
// [1,2].slice(1,9) 。slice函数第二个参数溢出，也能正常使用
res.push(Math.max(...nums.slice(left,right+1)))
// 推动左指针
left++
}
}
return res
};上面算法时间复杂度是O(kn)，其中k是在窗口中找到最大值的复杂度
双端队列
该算法将O(k)优化到O(1)，在单调队列中维护着单调递减数据，每次取值仅需取队首即可
视频讲解：https://www.bilibili.com/video/BV1bM411X72E/?p=27&spm_id_from=pageDriver
双端队列 = 单调栈的思路+栈底出栈（维护窗口大小）
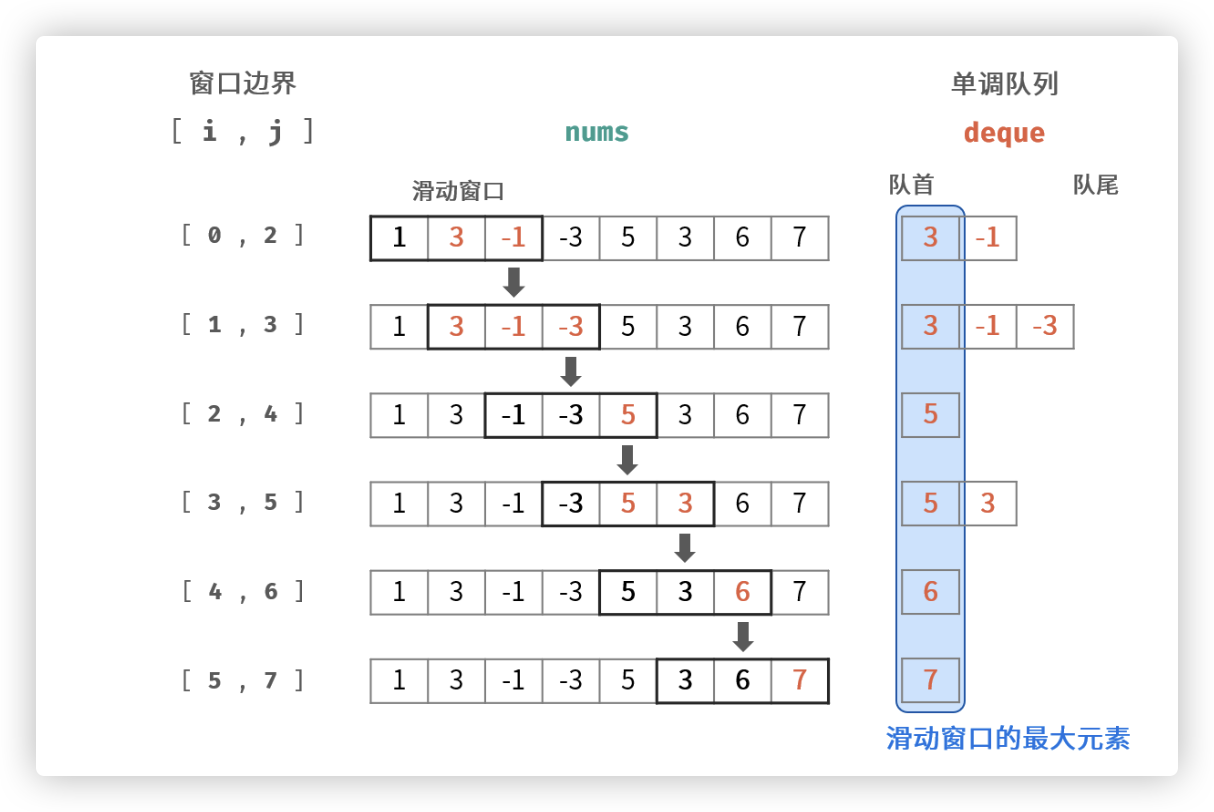
这个图一步步描述了滑动窗口移动时，对应的单调队列的变化
看下面代码两点注意：
- 按顺序变量的nums数组，i看作是窗口右端点。每轮for循环对应窗口移动1次
- 我们从1次for循环入手分析，队尾比新人小，就一直删队尾，队头超出窗口区间就删掉
- 队列中从队尾入队，从队首出队，其中仍然是数组顺序（只不过，队列不连续了，因为有些在队尾出去了）
js
var maxSlidingWindow = function(nums, k) {
let deque=[] //单调递减。存的是nums的索引
let ans=[]
for (let i=0;i<nums.length;i++){
// 不符合单调递减，队尾一直出队
while (deque.length>=1&&nums[deque[deque.length-1]]<nums[i]){
deque.pop()
}
// 符合单调递减，再入队索引
deque.push(i)
// 队头是最大值，但是如果队头在窗口之外，要剔除
while (deque[0]<=i-k){
deque.shift()
}
// 经过上面两个while的维护，到这里deque内元素个数是k个（即窗口大小）
// 存入答案 注意：索引i，是第i+1个数，必须>=k个了，才开始存答案
if (i+1 >= k ) ans.push(nums[deque[0]]);
}
return ans
};递归问题
递归分析
递归是什么？
递归是一种编程技巧，代码上具体表现为函数自己调用自己。分治算法、回溯算法都是应用递归技巧的具体案例
递归问题的核心？
写一层逻辑，这一层逻辑反复执行（类似for循环），本层将结果向上层return
代码逻辑分析：
最后一层（根据条件判断是否为最后一层，return最后一层结果），也叫递归终止条件
最后一层找不到？看下递归函数 f(n)->f(n-1)，看下递归的入参一层层下移最后会变成啥，就是最后一层的条件
其余每层公用的逻辑（return是返回上一层的结果）
层与层之间的通讯
return通讯： n+1层 ---> n层 发送数据。这个数据会最终返回最顶层，即从下到上（2-1注释）
注意并不是所有题的答案都必须return到顶层。有可能定义个全局变量，然后在每一层中做逻辑，最后答案是这个值。例如，定义全局变量max，每层比较大小存入最大值，最后返回这个最大值
递归入参通讯：n+1层 <--- n层 发送数据。每一层的入参，一般都用来标识本层的一些信息，比如自己是第几层。即从上到下（2-2注释）
很多题是很难看出来每一层是什么，所以将递归问题转换为层次图，会更为直观分析
js
recursion(params)// 这里是顶层，即0层
function recursion(params){
// 1、最后一层的处理逻辑
if(最后一层){
return xxx
}
// 2、其余任意一层的处理逻辑 （这里能看到两层，既然是任意层，为了方便，假设当前层为0层）
// 2-1 这一层的递归函数recursion，就是第1层。latter就是1层返回的值
const latter=recursion(params) // 我们可以对上一层的参数params进行处理，传入下一层
// 2-1 这里是当前层的逻辑，即0层
return 处理latter后的数据
}斐波那契
F(n)=F(n-1)+F(n-2)
层次图
js
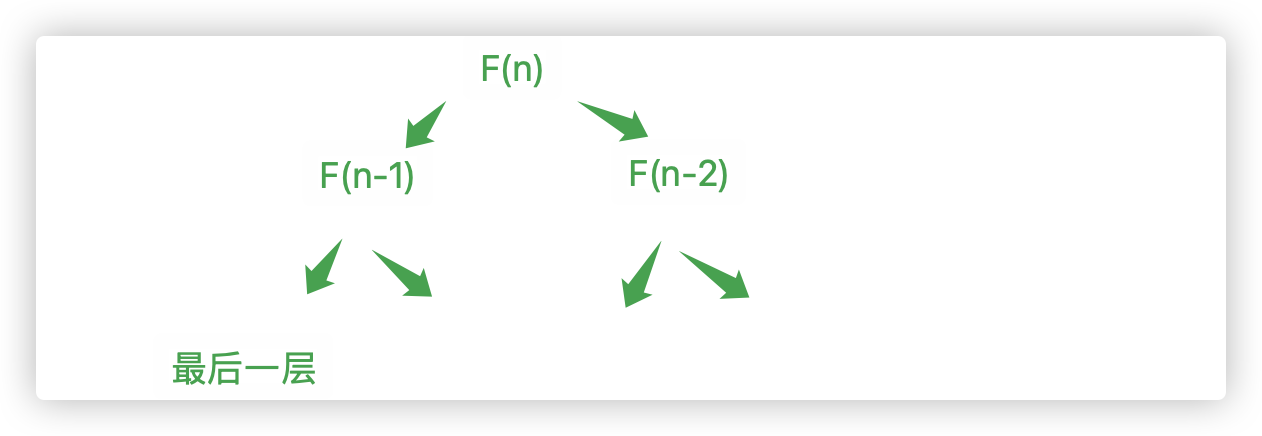
function fin(n){
// 最后一层 ，fin(n) ->fin(n-1)、fi(n-2)，n会一步一步变成0、1
if(n===0||n==1){
return n
}
// 本层。这里直接return就行（写latter是为了更清晰）
const latter=fin(n-1)+fi(n-2)
return latter
}阶乘
n!=n*(n-1)*(n-2)...*1
这题看不出来树状层次，需要我们抽象出来函数。f(n)=n*f(n-1)=n*(n-1)*f(n-2)zh
js
function factorial(n){
if(n===1) return 1
return n*factorial(n-1)
}树的部分
参加树章节dfs的题
分治
分治将一个较大的问题分解成多个相对较小的子问题，这些子问题通常与原始问题具有相同的结构。然后，将子问题的解合并起来，形成原始问题的解
例如：快速排序、归并排序
模板：
这里就可以看出来分治算法使用的是递归技巧，其核心是在当前层 合并下一层，即前面提到的return通讯
js
function divide_conquer(problem, param1, param2, ...){
if(problem === null){
// return result
}
//分割问题
subproblem = split_problem(problem, data)
//计算子问题
subResult1 = divide_conquer(subproblem[0], p1, ...)
subResult2 = divide_conquer(subproblem[1], p1, ...)
subResult3 = divide_conquer(subproblem[2], p1, ...)
...
result = process_resule(subResult1, subResult2, subResult3,...)
}50. Pow(x, n)
分治
js
var myPow = function(x, n) {
if (n===0){
return 1
}else if (n===1){
return x
}else if (n<0){
return myPow(1/x,-n)
}else{
if (n%2===0){
return myPow(x*x,n/2)
}else {
return x*myPow(x,n-1)
}
}
};递归
js
var myPow = function(x, n) {
if(n===0){
return 1
}
return myPow(x,n-1)*x
};对比看下 递归、分治还是有区别的
169. 多数元素
哈希计数
js
var majorityElement = function(nums) {
let hash={}
for(let val of nums){
if(!hash[val]){
hash[val]=0
}
hash[val]++
}
for (let key of Object.keys(hash)){
if (hash[key]>Math.floor(nums.length/2)){
return key
}
}
return ''
};124. 二中的最大路径和
解
js
var maxPathSum = function(root) {
let max=-Infinity
const dfs=(root)=>{
// 如果本层是递归出口，返回上层的值
if (root===null){
return 0
}
// 本层计算结果的逻辑
let leftChildMax=dfs(root.left)
let rightChildMax=dfs(root.right)
max= Math.max(max,root.val+leftChildMax+rightChildMax)
// 本层返回上层的值 ( 本层的最大值 )
const curValue=root.val+Math.max(leftChildMax,rightChildMax)
return curValue>0?curValue:0
// 注意这里为啥小于0，return 0 呢。参考下面用例：
// [2,-1] 正确结果2。如果不设置这句，直接返回curValue，结果就是1
// 因为这题要求最大值，返回给上层的一定不能是负数
}
dfs(root)
return max
};
// // res=:253. 最大子数组和
滑动窗口：
这个题难在如何维护窗口
先将nums[right]加入窗口，在调整窗口到符合条件
js
var maxSubArray = function(nums) {
let left=0,right=0
let sum=0,max=-Infinity
for (;right<nums.length;right++){
// 加入滑动窗口
sum+=nums[right]
max=Math.max(max,sum)
// 维护窗口 保证sum+=nums[right]其中原sum必须为证书，nums[right]>sum就是这个含义
// 一开始错误的想法：一直判断left指向的值，小于0就一直收缩窗口。
// [1,-2]这种情况，left是正数，但是窗口内仍有负数-2
while (nums[right]>sum){
sum-=nums[left]
left++
max=Math.max(max,sum)
}
}
return max
};先调整到符合条件，再放入right。注意：sum初始值为0（或者移动窗口过程中窗口没有元素了，也会出现sum为0），这时如果max是个负数，那么通过max=Math.max(max,sum) 来确定最大值就是0了，但是实际上应该是那个负数。这种情况需要特别处理
对于上面为什么可以规避这个问题我不太确定，只是查到Kadane算法，貌似：
sum出现负数就重置为0，就能使得max = Math.max(max, sum)永远成立
Kadane算法max初始化为第一个元素，我简单测试了下max初始化为-Infinity应该也是对的
for循环中还会再次取出nums[0]与max作比较，虽然用了nums中的元素但是并不影响for循环的逻辑
js
var maxSubArray = function(nums) {
let max = nums[0];
let sum = 0;
for (let i = 0; i < nums.length; i++) {
if (sum < 0) {
sum = 0; // 重置为0，因为负数会降低子数组的和
}
sum += nums[i];
max = Math.max(max, sum);
}
return max;
};js
var maxSubArray = function(nums) {
const len =nums.length
let left=right=0
let max=-Infinity
let sum=0
for (;right<len;right++){
// 放入right前，将窗口维护为和>=0
while(sum<0){
sum-=nums[left]
// 这种方式需要特别处理
if (sum!==0){
max=Math.max(max,sum)
}
left++
}
// 符合条件了，放入right
sum+=nums[right]
max=Math.max(max,sum)
}
return max
};动态规划
js
var maxSubArray = function(nums) {
// dp[i] 是 0-i 范围子数组的最大和
// dp[0]=nums[0]
let dp=new Array(nums.length).fill(-Infinity)
dp[0]=nums[0]
for (let i = 0; i < nums.length; i++) {
if (dp[i]>0){
dp[i+1]=dp[i]+nums[i+1] // nums[i+1] 无论正负，都要加上，否则后续的dp就不连续了
}else {
dp[i+1]=nums[i+1]
}
}
dp.sort((a,b)=>b-a)
return dp[0]
};938. 二叉搜索树的范围和
递归
js
var rangeSumBST = function(root, low, high) {
if (root===null){
return 0
}
if (root.val<low){
return rangeSumBST(root.right,low,high)
}
if (root.val>high){
return rangeSumBST(root.left,low,high)
}
if(root.val>=low&&root.val<=high){
return root.val+rangeSumBST(root.right,low,high)+rangeSumBST(root.left,low,high)
}
return max
};回溯
js
// 问题1：从str1、str2各选一个字符，共有多少组合？
let str1='abc'
let str2='def'
// 答：常规思路，双层for循环嵌套
for(let val1 of str1){
for(let val2 of str2){
}
}
// 问题2：从str1、str2、....strn中各选一个字符，共有多少组合？
// n层for循环怎么写？可见单纯的for表达能力有限，递归与for循环相似下面这种增量构建答案的思路就是回溯
一般用变量path存储一条完整的路径，将其推入结果变量ans中，重复下去直到所有path都被推入ans
如下图，[a,d]、[a,e]、[a,f] 等都是完整的路径。结果path中包含全部的路径
代码如何实现？
前面提到过递归的通讯方式有一种是入参：我们可以传入[]作为path，在每层依次收集路径上的元素（选1个加入path），到最后一层推入ans即可
for循环一行 a、b、c，每个元素都是一个同级的递归函数。每个递归函数分别下下一级递归（这种思路显著与传统递归思路不同，传统递归思路都是一个递归函数，一直向下一级递归）
这里在语法上有个易错点，需要将path拷贝一份推入ans中。path是个引用类型，拷贝可以避免其他递归分治修改path导致ans变化的情况
创建多个同级的递归，如果存在不满足题意的递归，我们可以不创建提高效率（这就是枝剪，这个词有些误导，我们只能设置递归终止，但是并不可以中断递归过程；所谓枝剪只是不创建不符合题意的递归）
回溯是一种试探性的搜索算法，它会尝试增量构建一个解，如果解不可行就回退到之前的状态并尝试其他选项（当回溯用于树的时候，就是深度优先搜索DFS）
分治是将大问题分解为结构一样的小问题求解，小问题合并为新的解，最后保留一个解
而回溯是其他问题的解增量构建为新的解。保留多个解的集合
回溯模板
js
ans = [];
function backtrack (level,path) {
if (最后收尾) // 判断此时path已收集完整
ans.push(path.slice()); // 这里必须拷贝一份path，否则ans放入引用类型，path后续修改会影响到ans
return // 这里的return只是结束递归。
}
// 其余任意层(假设为0层)
// 在回溯中通过ans、path记录答案。不必通过return来传递数据
// 创建多个同级的递归函数
// 任意层核心是维护path，将符合添加的数据加入path
path.push(xxx)
backtrack(level+1,path) // 1层的递归
backtrack(level+1,path) // 1层的递归
}
backtrack(0,[])回溯问题分为求子集、求组合、求排列回溯
子集型
两种思路（选取哪种思路还有根据题而确定）
- 从输入角度。每一个输入值选、不选两种可能（对应就是集合中有、没有这个值）
- 从答案角度。叶子节点是答案（完整的path就是从根到叶子节点的路径上的所有点）
78题的图，输入角度看线、答案角度看方块
78. 子集
题目
2刷感悟：这个题通过选、不选可以将数据收集到path，如果题目不是求子集，而是只保留有k个元素的子集，我们只需在最后一层的判断条件上 增加一个条件，即path=k
js
if(curIndex===nums.length|| path ===k )js
//给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
// 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。递归思路：在return放置每层的结果。这里的参数是辅助通知当前层是哪层
js
var subsets = function(nums) {
function recursion(curIndex){// 0层
// 最后一层
if (curIndex===nums.length-1){
return [[],[nums[curIndex]]]
}
// 其余层（假设当前为1层）
// 2层
const latterList=recursion(curIndex+1) //如果分不清latterList到底啥样子，可以看下最后一层的返回值
// 1层 （nums[curIndex]有和没有两种情况）
let temp=[]
for (let itemList of latterList){
temp.push([nums[curIndex],...itemList])
}
return [...temp,...latterList]
}
return recursion(0)
};
subsets([0])递归思路：全员变量存储
js
var subsets = function(nums) {
let ans=[]
function recursion(curIndex){
// 最后一层
if (curIndex===nums.length-1){
ans= [[],[nums[curIndex]]]
return
}
// 其余层（假设当前为0层）
// 1层
recursion(curIndex+1)
// 0层 （nums[curIndex]有和没有两种情况）
let temp=[]
for (let itemList of ans){
temp.push([nums[curIndex],...itemList])
}
ans = [...temp,...ans]
}
recursion(0)
return ans
};回溯解法1：从输入的角度（选、不选）
注意：为什么这题有恢复现场的逻辑，而17没有呢？
17题不是push数据到path中，而是通过path[i]=xx覆盖path中的值，这样每一层递归都是覆盖
时间复杂度：o(n*2^n) ，可以看其余层代码，这一层执行了2个同级递归（实际含义：每层选、不选两种情况，共n层，就是2^n），注意还有 slice 拷贝的复杂度o(n)，最后就是o(n*2^n) 了
空间复杂度：o(n)
js
var subsets = function(nums) {
let ans=[]
function backtrace(curIndex,path){
// 最后一层
if (curIndex===nums.length){ // 与17题一致，都是因为num最后一个数与前面的处理逻辑一致，所以这里多补了一层用来将path存入ans
ans.push(path.slice())
return
}
// 其余层
// 例如 nums=[1,2],curIndex=0。第一个数是否加入path？这里就出现了2个同级递归函数
// 不选，跳过
backtrace(curIndex+1,path)
// 选，加入path
path.push(nums[curIndex])
backtrace(curIndex+1,path)
path.pop()
// 为啥pop？一些文章里称这里为“恢复现场”，这里pop出来的是什么，不太好想。我们可以假设当前层是`倒数第2层`，push推入了最后一个数，backtrace完成了将path推入ans，pop就是将最后一个数推出。这样`倒数第3层`的path就是正常的。pop就是回溯的核心，即每一层都是尝试一个分支，然后再回退
}
backtrace(0,[])
return ans
};回溯解法2：从答案的角度，因为答案是子集，每次递归的path都是一个解（求[1、2、3]的子集，如果[1]是一个子集，[1、2]也是一个子集）
js
var subsets = function(nums) {
let ans=[]
function backtrace(curIndex,path){
// 最后一层
if (curIndex===nums.length){
return
}
// 其余层
// 每一层递归都是一个解，推入ans中
ans.push(path.slice())
for (let i=curIndex;i<nums.length;i++){
path.push(nums[i])
backtrace(i+1,path) // 下一层起始点为i+1,每次都只往后找，这是为了避免重复
path.pop()
}
}
backtrace(0,[])
return ans
};17. 电话号码的字母组合
层次图：
回溯法：从答案的角度
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]每个元素是一个解将其存储在path中，以"ad"这个解为例子，a是按键2的字母，d是按键3的字母
计算path时，只需要将2的所有值for循序，进入下一层递归将3的所有值for循环
js
var letterCombinations = function(digits) {
const record={
2:'abc',
3:'def',
4:'ghi',
5:'jkl',
6:'mno',
7:'pqrs',
8:'tuv',
9:'wxyz'
}
let ans=[]
// 用例"",计算的ans=[[]]，结果返回 [""],正确结果是[]。所以这里过滤掉
if(digits===''){
return []
}
function dfs(curIndex,path){
// 最后一层
if(curIndex===digits.length){
ans.push(path.slice())
return
}
// 其余层
for (let char of record[digits[curIndex]]){
path.push(char)
dfs(curIndex+1,path)
path.pop()
}
}
dfs(0,[])
return ans.map(item=>item.join(''))
};131. 分割回文串
2刷感悟：正常情况下dfs是枚举所有字符的组合，但是这题通过选不选逗号，记录 startIndex、endIndex，可实现筛选连续字符串
回溯1：输入视角，每两个连续字符之间逗号选与不选
这题需要记录下起点和终点，判断两个之间是否为回文。所以入参有两个index
js
var partition = function(s) {
let ans=[]
function backtrace(startIndex,endIndex,path){
// 最后一层
if (endIndex===s.length){
ans.push(path.slice())
return
}
// 任意层
// 不加逗号
if (endIndex<s.length-1){
// 当到最后一个(curIndex===s.length-1)时，字符串结束，相当于是必加逗号。所以用if扣掉这种情况
backtrace(startIndex,endIndex+1,path)
}
// 加逗号
const temp=s.slice(startIndex,endIndex+1) // 例如结果为[ [xxx],[yyy] ]，判断xxx是回文才加入path
if (temp===temp.split('').reverse().join('')){ // 是回文
path.push(temp)
backtrace(endIndex+1,endIndex+1,path)
path.pop()
}
}
backtrace(0,0,[])
return ans
}回溯2：答案视角。记录字符串结束位置
例如：输入aab
- 结束位置是a的，判断是回文，加入path迭代剩下的
- a，判断是回文，加入path
- b，判断是回文，加入path。得到结果[a,a,c]
- 结束位置是aa的，判断是回文，加入path迭代剩下的
- b ，判断是回文，加入path。得到结果[aa,b]
- 结束位置是aab的，判断不是回文剪枝了
js
var partition = function(s) {
let ans=[]
function backtrace(endIndex,path){ // endIndex每个子串结束的位置
// 最后一层
if (endIndex===s.length){
ans.push(path.slice())
return
}
// 任意层
for (let i=endIndex;i<s.length;i++){
const temp=s.slice(endIndex,i+1)
if (temp===temp.split('').reverse().join('')){ // 是回文
path.push(temp)
backtrace(i+1,path)
path.pop()
}
}
}
backtrace(0,[])
return ans
};组合型
组合型问题本质就是长度固定的子集型问题
77. 组合
题目
js
//给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
//
// 你可以按 任何顺序 返回答案。递归思路：return返回每层结果。这题难点在其余层的公用逻辑。这题存入全局变量的解法与前面都是一致的就省略了
js
var combine = function(n, k) {
let targetList=[]
for (let i=0;i<n;i++ ){
targetList.push(i+1) }
function recursion(k){
// 最后一层
if (k===1){
// 例如n=4，k=1。这里就应该是[[1],[2],[3],[4]]
let temp=[]
for (let i=0;i<n;i++ ){
// 必须让数据从小到大。在其余层中也要保持这个规律
temp.push([i+1])
}
return temp
}
//-------------------
这里举个例子讲下思路：
假设 n=4,k=3
k=2时，结果为 [[1,2], [1,3], [1,4],[2,3]，[2,4], [3,4]]
k=3时，
* 以下一层第1个元素[1,2]为例子，剩下的元素为3、4。k=3时能组合成[1,2,3]、[1,2,4]
* 以下一层第2个元素[1,3]为例子，剩下的元素为2、4。k=3时能组合成[1,3,2]、[1,3,4]。这里重点，这里的[1,3,2]与上一个中的[1,2,3]重复了，所以我们要保持每一层的子数组必须从小到大，然后找剩下元素中大于子数组最后元素的加入
//-------------------
// 其余层
latterList=recursion(k-1) // 1层 ，latterList的结构分不清，可以假设1层就是最后一层，看下最后一层的返回值
let temp=[]
for (let itemList of latterList){
// 这里比较复杂，需要看下举的例子
const restList=targetList.filter(item=>{
return item>itemList[itemList.length-1]
})
for (let rest of restList){
temp.push([...itemList,rest])
}
}
return temp
}
return recursion(k)
};回溯1：从输入角度，每一层都是分为当前元素是否选择加入path
题目中需要剪枝，思路就是下面这个 n-(k-path.length)+1
js
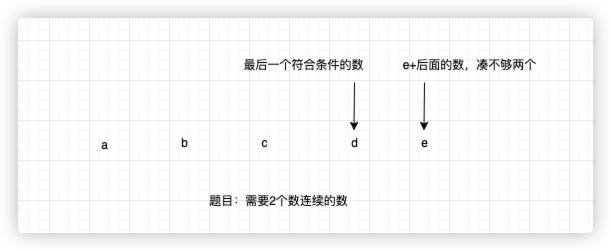
var combine = function(n, k) {
let ans=[]
function backtrace(curIndex,path){
// 最后一层
if (path.length===k){
ans.push(path.slice())
return
}
// 其余任意层
// 是否选curIndex位置的数字，加入path
// 在当其层，restLen是凑够k个，还剩余的个数
let restLen= k-path.length
// 这个if做了枝剪，符合的递归才会创建
// n-restLen+1是 最后一个符合条件数的到第1个数的长度
// (n-restLen+1)-1 是把长度变成索引
if (curIndex<=(n-restLen+1)-1){
// 不加入
backtrace(curIndex+1,path)
// 加入
path.push(curIndex+1) // curIndex+1 是 curIndex 位置的数字
backtrace(curIndex+1,path)
path.pop()
}
}
backtrace(0,[])
return ans
};回溯2：从答案角度，答案是： 多个长度k的数组
图里的圈就是一个解（path收集的路径），我们不再从输入的角度，去考虑1-n的每一位选与不选，而是从解的角度分析每层递归还有哪些值可以选，用for循环出来
if最后终止的条件页
js
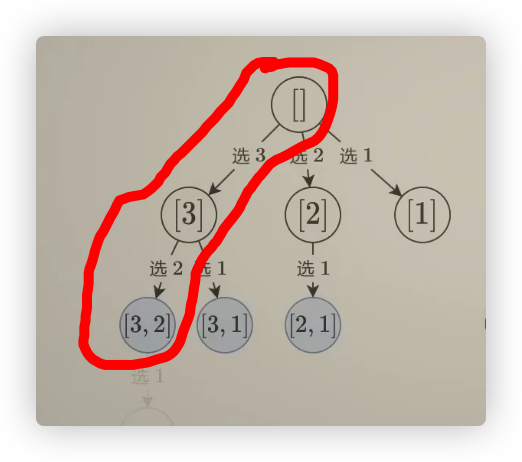
var combine = function(n, k) {
let ans=[]
function dfs(startPos,path){
// 最后一层
if(path.length===k){
ans.push(path.slice())
return
}
for (let i=startPos;i<=n;i++){ // 本层可选的数字
path.push(i)
dfs(i+1,path) // 下一层从下一个数开始，避免一个数被加入两次
path.pop()
}
}
dfs(1,[])
return ans
};
// --- 优化
var combine = function(n, k) {
let ans=[]
function backtrace(curIndex,path){
// 最后一层
if (path.length===k){
ans.push(path.slice())
return
}
// 其余任意层
let restLen= k-path.length
for (let i=curIndex;i<=(n-restLen+1)-1;i++){
path.push(i+1) // 当前层 for 循环把所有可能都枚举了
backtrace(i+1,path)
path.pop()
}
}
backtrace(0,[])
return ans
};216. 组合总和 III
题目
js
//找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：
//
//
// 只使用数字1到9
// 每个数字 最多使用一次
//
//
// 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。回溯：输入角度，选不选
输入角度第一个解法是每凑够一个path才判断一次
而第二种解法将sum作为参数，每次都计算，不符合要求的分支被提前剪枝，理论性能更优秀。推荐第二种方法，在递归构成中剪枝
js
var combinationSum3 = function(k, n) {
let ans=[]
function backtrace(startIndex,path){
// 最后一层
if (path.length===k){
// 这里计算了一下path元素之和是否为n
let temp=0
for (let i=0;i<k;i++){
temp+=path[i]
}
if (temp===n){
ans.push(path.slice())
}
return
}
// 其余任意层
if(startIndex<=(9-(k-path.length)+1)-1){//剪枝。与77剪枝思路一致
// 不选
backtrace(startIndex+1,path)
// 选
path.push(startIndex+1)
backtrace(startIndex+1,path)
path.pop()
}
}
backtrace(0,[])
return ans
};
// 也可以把数组求和的sum，一层一层传下去。比上面多了一个剪枝规则
var combinationSum3 = function(k, n) {
let ans=[]
function backtrace(startIndex,sum,path){
// 最后一层
if (path.length===k){
if (sum===n){
ans.push(path.slice())
}
return
}
// 其余任意层
if(startIndex<=(9-(k-path.length)+1)-1){//剪枝。与77剪枝思路一致
// 不选
backtrace(startIndex+1,sum,path)
// 选
if (sum<=n){//剪枝。如果path元素和超过了n，不符合题意需要剪枝下
path.push(startIndex+1)
sum+=(startIndex+1)
backtrace(startIndex+1,sum,path)
path.pop()
sum-=(startIndex+1)
}
}
}
backtrace(0,0,[])
return ans
};答案角度：剩下的选一个加入path，for循环剩下的，把所有答案尝试下
js
var combinationSum3 = function(k, n) {
let ans=[]
function backtrace(startIndex,sum,path){
// 最后一层
if (path.length===k){
// 这里计算了一下path元素之和是否为n
if (sum===n){
ans.push(path.slice())
}
return
}
// 其余任意层
for (let i=startIndex;i<=(9-(k-path.length)+1)-1;i++){//剪枝
if(sum<=n){// 剪枝
path.push(i+1)
sum+=(i+1)
backtrace(i+1,sum,path)
path.pop()
sum-=(i+1)
}
}
}
backtrace(0,0,[])
return ans
};22. 括号生成
回溯解法：从输入角度，选( 或者选 )
原本我的解法是在最后一层中通过栈来判断是否满足括号匹配（有左括号就入栈，遇到右括号就出栈，最后栈为，则证明括号匹配），结果Maximum call stack size exceeded（栈溢出了）
所以，递归过程中剪枝
放入左括号没有限制
放入右括号：当前子串的右括号数<左括号数，才能加入右括号 ，这个条件能保证每层的子串都是有效的
剪枝左括号、右括号都<n
2*n个括号，所以左、右括号最多也就是n个，超过n个肯定无效
js
var generateParenthesis = function(n) {
let ans=[]
// curIndex 当其第几个元素
// leftBracketCount 左括号的个数。与216输入视角的第二种解法思路一样，通过参数在各层之间统计数据，提前剪枝
// path 收集路径上的节点
function backtrace(curIndex,leftBracketCount,path){
// 最后一层
if (curIndex===2*n){
ans.push(path.join(''))
return
}
// 其余任意层
// 选(
if (leftBracketCount<n){// 剪枝
path.push('(')
leftBracketCount++
backtrace(curIndex+1,leftBracketCount,path)
path.pop()
leftBracketCount--
}
// 选)
const rightBracketCount= path.length-leftBracketCount
if (rightBracketCount<n&&rightBracketCount<leftBracketCount) {//剪枝，只有左括号数>右括号数，才仍加入右括号
path.push(')')
backtrace(curIndex + 1, leftBracketCount, path)
path.pop()
}
}
backtrace(0,0,[])
return ans
}从答案视角：
题解地址 枚举左括号的位置，没太看明白，后续研究下
排列型
46. 全排列
从输入角度，每个位置只能有nums.length个可能（剪枝掉一些情况，实际会小于这个值）
2刷感悟：我们用递归处理这个数组，本质上就是元素任意组合，但是这个题要求全排列就只是元素位置变化，不能有元素缺失，所以从输入角度看只有选一条路，不能不选。
还有就是，下面的path.includes是防止重复
js
var permute = function(nums) {
let ans=[]
function backtrace(curIndex,path){
// 最后一层
if (curIndex===nums.length){
ans.push(path.slice())
return
}
// 其余任意层
for (let val of nums){
if (!path.includes(val)){ // 剪枝 。例如 [1,x,x]，第一位是1了，后面两位就不能出现1了
path.push(val)
backtrace(curIndex+1,path)
path.pop()
}
}
}
backtrace(0,[])
return ans
};排列型问题，curIndex位置应该是在剩余集合中选元素。例如 [1,x,x]，第一位是1了，后面两位就不能出1了。后面一位，只用枚举nums中就要剔除1剩余的元素
上面解法用户include方法判断，只枚举path中不存在的元素
我们还可以利用 递归的入参通讯，把剩余数据传递到每一层
题目说了nums内容不重复，所以可用set，但是该思路用JS实现会超时
js
var permute = function(nums) {
let ans=[]
function backtrace(curIndex,restSet,path){
// 最后一层
if (curIndex===nums.length){
ans.push(path.slice())
return
}
// 其余任意层
for (let val of restSet){
path.push(val)
restSet.delete(val)
backtrace(curIndex+1,restSet,path)
path.pop()
restSet.add(val)
}
}
backtrace(0,new Set(nums),[])
return ans
};思路是一样的，我们也可以不使用set，使用一个数组记录是否访问过。 visitList[i]为true，代表nums[i]被访问过
js
var permute = function(nums) {
let ans=[]
function backtrace(curIndex,visitList,path){
// 最后一层
if (curIndex===nums.length){
ans.push(path.slice())
return
}
// 其余任意层
for (let index in visitList){
if (visitList[index]){
path.push(nums[index])
visitList[index]=false
backtrace(curIndex+1,visitList,path)
path.pop()
visitList[index]=true
}
}
}
const visitList = new Array(nums.length).fill(true)
backtrace(0,visitList,[])
return ans
};迭代法与递归法
递归在数理逻辑上总是能转化为迭代的
递归：
- 代码结构：函数调用自身
- 结束方式：递归只能到最后一层终止，无法在任意中间节点终止递归
- 效率：大量重复计算，效率低。可以用剪枝、记忆化来提高效率
迭代：
- 代码结构：使用for循环结构反复执行一组指令。for循环外部定义变量，每次迭代将数据存下来，作为下一步的输入，一步步逼近正确答案
- 结束方式：任意位置设置终止条件，for循环会直接退出
- 效率：高于一般的递归（未使用优化方法的递归）
斐波那契
js
// 递归
function fin(n){
// 最后一层 ，fin(n) ->fin(n-1)、fi(n-2)，n会一步一步变成0、1
if(n===0||n==1){
return n
}
// 本层。这里直接return就行（写latter是为了更清晰）
const latter=fin(n-1)+fi(n-2)
return latter
}
// 迭代
function fin(n){
// 前两项分别为0和1
if (n == 0) return 0;
if (n == 1) return 1;
// 初始的前两项值
int fib0 = 0;
int fib1 = 1;
int fibResult = 0;
// 从第三项开始迭代计算
for (int i = 2; i <= num; i++)
{
// 当前项等于前两项之和
fibResult = fib0 + fib1;
// 更新前两项的值
fib0 = fib1;
fib1 = fibResult;
}
return fibResult;
}阶乘
js
// 递归
function factorial(n){
if(n===1) return 1
return n*factorial(n-1)
}
// 迭代
function factorial(n){
// 初始结果设为1
let result = 1;
// 迭代计算阶乘，从1到num逐步相乘
for (int i = 1; i <= n; i++){
result *= i;
}
return result;
}树的部分（待补充）
dfs回溯算法，如果使用迭代法，需要用到辅助栈。这块以后再补充
动态规划（迭代法）
好文介绍记忆化搜索到动态规划的内容
其中很重要的一段内容，区分了贪心和动态规划（递归搜索）的区别
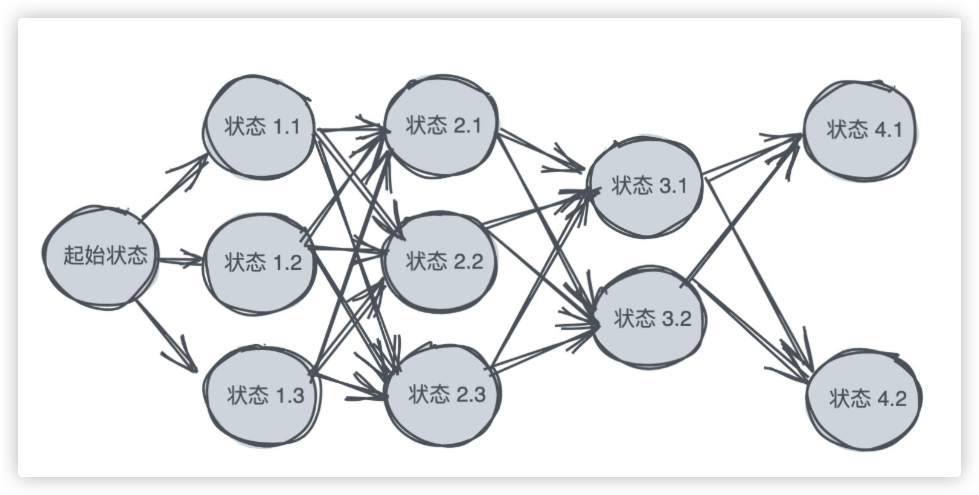
将问题每个阶段抽象为状态（用圆圈来表示），状态之间可能会发生转化（用箭头表示）。可以画出类似如下的图
那我们应该做出如何的决策序列才能使得结果最优？换句话说就是每一个状态应该如何选择到下一个具体状态，并最终到达目标状态。这就是动态规划研究的问题。
每次决策实际上不会考虑之后的决策，而只会考虑之前的状态。 形象点来说，其实是走一步看一步这种短视思维。为什么这种短视可以来求解最优解呢？那是因为：
- 我们将所有可能的转移全部模拟了一遍，最后挑了一个最优解。
- 无后向性（这个我们后面再说，先卖个关子）
而如果你没有模拟所有可能，而直接走了一条最优解，那就是贪心算法了
动态规划模版
js
function xxx(){
// 创建dp数组，一维数组or二维数组
// dp是递归转化来的，递归函数入参是几个，就是几维数组
dp=new Array(x).fill(y)
// 可直接确定的dp边界数据，可以直接给值
dp[0]=z
//
for(){
// 定义状态转移方程
// 动态规划就是最优决策的过程 本次决策的结果= option(上次决策的结果)
dp[i]= option(dp[i-1])
}
}记忆化搜索
记忆化搜索=递归+保存每一层递归结果
以下图斐波那契递归为例子，递归会将所有可能尝试一遍，其中存在大量重复的。我们可以将结果存在下来，来提高性能
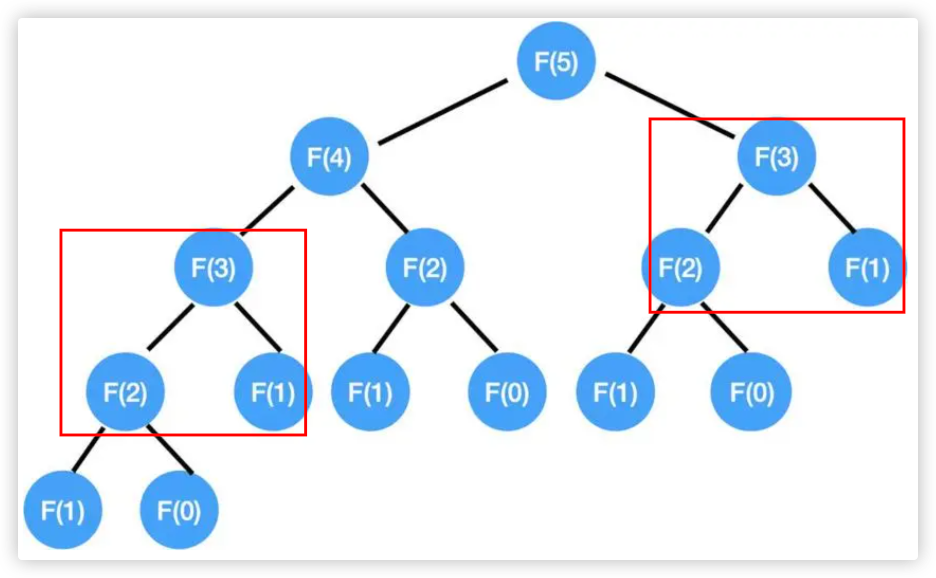
因为要时间记忆化（存储）每层结果，所以必须使用return通讯，将每层的结果返回出来并存储
动态规划其实就是记忆化搜索的一种形式
198. 打家劫舍
回溯：这题用回溯从输入角度会超时，因为回溯用的是递归入参数通讯，所以没法记忆化每层的结果
尝试剪枝仍然超时
js
var rob = function(nums) {
let max=0
function backtrace(curIndex,sum){
// 最后一层
if (curIndex>=nums.length){
max=Math.max(sum,max)
return
}
// 其余层
if (curIndex<=nums.length-1){
// 选
sum+=nums[curIndex]
backtrace(curIndex+2,sum)
sum-=nums[curIndex]
// 不选
backtrace(curIndex+1,sum)
}
}
backtrace(0,0)
return max
};用最经典的递归思路，return之前先存储下结果（这就是记忆化），就不会超时了
js
var rob = function(nums) {
let cache=new Array(nums.length).fill(-1)
function recursion(endIndex){
// 最后一层
if (endIndex<0){
return 0
}
// 其余层
if (cache[endIndex]===-1){
cache[endIndex] = Math.max(recursion(endIndex-1),recursion(endIndex-2)+nums[endIndex])
}
return cache[endIndex]
}
return recursion(nums.length-1)
};其实这等同于动态规划思路 ，上面是在递归中使用数组存储结果（322 递归函数有两个入参，我们可以使用map存储，将两个拼接上作为key）
我们可以转化为动态规划
使用for循环，直接用每层数据存入dp数组索引就是，递归函数也都换成dp
为什么不判断Math.max(dp[i-1],dp[i-2]+nums[i])中的两个dp数据是否存在，就直接赋值给 dp[i]？
i是从小到大的，dp[i]前面的数据一定是存在的
js
var rob = function(nums) {
if (nums.length===1){
return nums[0]
}
let dp=new Array(nums.length).fill(-1)
dp[0]=nums[0]
dp[1]=Math.max(nums[0],nums[1])
//因为地推中dp[i-2]，i最小就是2，所以从2开始
for (let i=2;i<nums.length;i++){
dp[i]= Math.max(dp[i-1],dp[i-2]+nums[i])
}
return dp[dp.length-1]
};背包问题
有0-1背包、完全背包两类问题
0-1背包
Capacity:背包容量
w[i]: 第i件物品的体积
v[i]: 第i件物品的价值
求：每个物品只能选1件或者不选，所选物品不超过Capacity的情况下，获取最大价值
常见题目变形：
最多装Capacity的情况，求方案数/最大价值和
恰好装Capacity的情况，求方案数/最大价值和/最小价值和
至少装Capacity的情况，求方案数/最小价值和js
思路：枚举选与不选两种可能，
回溯：在非最后一层的其他任意一层枚举选与不选两个递归，在每层处理sum，本层两个递归函数分别递归
0-1背包： 使用return通讯，本层返回最大值。在本层直接最比较两个递归值中的最大值return到上层
494. 目标和
回溯：输入视角，选+或-
js
var findTargetSumWays = function(nums, target) {
let count=0
function backtrace(curIndex,sum){
// 最后一层
if (curIndex===nums.length){
if (sum===target){
count++
}
return
}
// 其余任意层
// 选+
sum+=nums[curIndex]
backtrace(curIndex+1,sum)
sum-=nums[curIndex]
// 选-
sum-=nums[curIndex]
backtrace(curIndex+1,sum)
sum+=nums[curIndex]
}
backtrace(0,0)
return count
};背包问题：两个背包，一个背包放全部正数、另一个放全部负数
js
package_a - package_b = target;
package_a + package_b = sum;
=>解方程： package_a =(target+sum)/2
题目转化为：给定一个大小为package_a的背包，有多少种组合方式能把背包装满
注意题目说是元素使非负整数，所以target+sum肯定是偶数才符合条件js
完全背包
核心区别，可重复选
Capacity:背包容量
w[i]: 第i件物品的体积
v[i]: 第i件物品的价值
求：每个物品可以不选或选（可重复选），所选物品不超过Capacity的情况下，获取最大价值
常见题目变形：
最多装Capacity的情况，求方案数/最大价值和
恰好装Capacity的情况，求方案数/最大价值和/最小价值和
至少装Capacity的情况，求方案数/最小价值和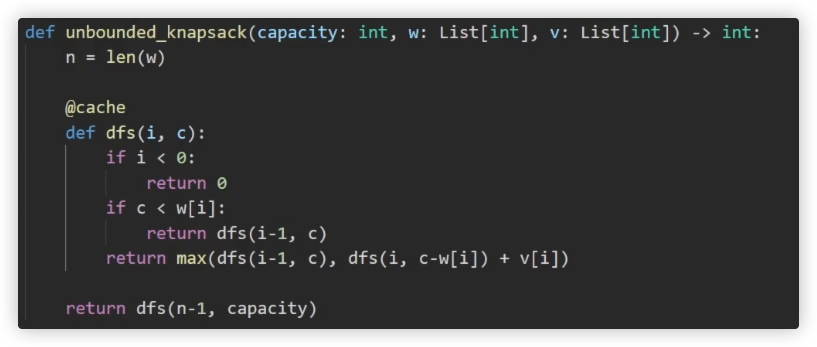
322. 零钱兑换
记忆化搜索，这里用map存储，当然也可以使用二位数组存储（行、列对应两个参数）
js
var coinChange = function(coins, amount) {
let cache=new Map()
function dfs(endIndex,amount){
// 最后一层
if (endIndex<0){
return amount===0?0:Infinity
}
// 其余层
const key= `${endIndex},${amount}` // 以两个入参拼接在一起，作为key缓存结果
if (amount<coins[endIndex]){// 剪枝，如果当前物品价值大于了背包剩余空间，就剪枝掉
if(!cache.has(key)){
cache.set(key,dfs(endIndex-1,amount))
}
return cache.get(key)
}else {
if(!cache.has(key)){
// dfs(endIndex-1,amount) 跳过
// dfs(endIndex,amount-coins[endIndex])+1 不跳过，可能加1
cache.set(key,Math.min(dfs(endIndex-1,amount),dfs(endIndex,amount-coins[endIndex])+1))
}
return cache.get(key)
}
}
const res= dfs(coins.length-1,amount)
return res===Infinity?-1:res
};动态规划，将计算结果存在dp数组中，这个题是需要缓存的函数是两个参数，所以得用二维数组
行、列分别对应两个参数。不在使用函数递归实现数据递归，而是for循环数组递推到最终的结果
如下图，数组的最后一个值就是结果
js
var coinChange = function(coins, amount) {
// dp[i][j] 凑成总和为i, 当前第j个面值的硬币，所需最少硬币个数
let dp=new Array(amount+1).fill(Infinity).map(()=>new Array(coins.length+1).fill(Infinity))
for (let i=0;i<=coins.length;i++){
dp[0][i]=0
}
for (let i=1;i<=amount;i++){
for (let j=1;j<=coins.length;j++){
// 把这里想成每一层，dp是用来存储每一层dfs递归函数返回值的。所以这里将dfs函数替换为dp
// 为什么不判断dp[x][y]存在后再赋值dp[i][j]？
// dp是for循环按顺序递推的，dp[i][j]前的值一定是有的
if (i>=coins[j-1]){
dp[i][j]=Math.min(dp[i][j-1],dp[i-coins[j-1]][j]+1)
}else{
dp[i][j]=dp[i][j-1]
}
}
}
return dp[amount][coins.length]===Infinity?-1:dp[amount][coins.length]
};进一步处理为一维dp数组，参考：https://github.com/azl397985856/leetcode/blob/master/thinkings/dynamic-programming.md
线性DP
1143. 最长公共子序列(LCS)
递归
前置思路：假设两个字符串text1、text2，此时text1指针指向字符x，此时text2指针指向字符y，递推有四种情况
- 选x，选y
- 选x，不选y
- 不选x，选y
- 不选x，不选y（都不选就是保持他自己，没有递推）
一般化：dfs的值表示回文字符串的长度，s、t分别是两个字符串
逻辑上是可以继续化简情况的
可以想下，
s[i]!=t[j]时，如果递归到了dfs(i-1,j)，他的下一层依旧是选不选的情况，下一层如果不选j，就是dfs(i-1,j-1)，所以包含了重复的情况
递归思路：
js
// ------超时------
var longestCommonSubsequence = function(text1, text2) {
function dfs(cur1,cur2){
// 最后一层
if (cur1<0||cur2<0){ // 注意这里要小于0，等于0还是符合其余层的计算规则的
return 0
}
// 其余层
if (text1[cur1]===text2[cur2]){
return dfs(cur1-1,cur2-1)+1
}else {
return Math.max(dfs(cur1-1,cur2),dfs(cur1,cur2-1))
}
}
return dfs(text1.length-1,text2.length-1)
};
// ------使用记忆化------
var longestCommonSubsequence = function(text1, text2) {
let cache = new Map()
function dfs(cur1,cur2){
// 最后一层
if (cur1<0||cur2<0){ // 注意这里要小于0，等于0还是符合其余层的计算规则的
return 0
}
// 其余层
if (text1[cur1]===text2[cur2]){
const key=`${cur1-1},${cur2-1}`
if (!cache.has(key)){
cache.set(key,dfs(cur1-1,cur2-1))
}
return cache.get(key)+1
}else {
const key1=`${cur1-1},${cur2}`
const key2=`${cur1},${cur2-1}`
if (!cache.has(key1)){
cache.set(key1,dfs(cur1-1,cur2))
}
if (!cache.has(key2)){
cache.set(key2,dfs(cur1,cur2-1))
}
return Math.max(cache.get(key1),cache.get(key2))
}
}
return dfs(text1.length-1,text2.length-1)
};动态规划
js
var longestCommonSubsequence = function(text1, text2) {
const len1=text1.length
const len2=text2.length
// 为什么二位数组大小是 （len1+1） *（len2+1）？
// dp[0][j] 或 dp[i][0] 表示其中一个字符串为空字符串的情况
const dp=new Array(len1+1).fill(0).map(()=>new Array(len2+1).fill(0))
// t e x t 2
// t
// e
// x
// t
// 1
for (let i=1;i<=len1;i++){
for (let j=1;j<=len2;j++){
// 为什么是text1[i-1]、text2[j-1] ？
// dp[i][j]是 text1从索引0到i-1，text2从索引0到j-1
if (text1[i-1]===text2[j-1]){
dp[i][j]=dp[i-1][j-1]+1
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
}
}
}
return dp[len1][len2]
};72. 编辑距离
操作的是i，
dfs(i,j-1)这个为什么是插入？dfs(i-1,j-1)的基础上i增加了一位
js
// 递归 超时
var minDistance = function(word1, word2) {
let len1=word1.length
let len2=word2.length
function dfs(endIndex1,endIndex2){
// 最后一层
if (endIndex1<0){
return endIndex2+1
}
if (endIndex2<0){
return endIndex1+1
}
// 其余层
if (word1[endIndex1]===word2[endIndex2]){
return dfs(endIndex1-1,endIndex2-1)
}else{
return Math.min(dfs(endIndex1,endIndex2-1),dfs(endIndex1-1,endIndex2),dfs(endIndex1-1,endIndex2-1))+1
}
}
return dfs(len1-1,len2-1)
};
// 记忆化
var minDistance = function(word1, word2) {
let cache=new Map()
let len1=word1.length
let len2=word2.length
function dfs(endIndex1,endIndex2){
// 最后一层
if (endIndex1<0){
return endIndex2+1
}
if (endIndex2<0){
return endIndex1+1
}
// 其余层
if (word1[endIndex1]===word2[endIndex2]){
const key=`${endIndex1-1},${endIndex2-1}`
if(!cache.has(key)){
cache.set(key,dfs(endIndex1-1,endIndex2-1))
}
return cache.get(key)
}else{
const key1=`${endIndex1},${endIndex2-1}`
const key2=`${endIndex1-1},${endIndex2}`
const key3=`${endIndex1-1},${endIndex2-1}`
if (!cache.has(key1)){
cache.set(key1,dfs(endIndex1,endIndex2-1))
}
if (!cache.has(key2)){
cache.set(key2,dfs(endIndex1-1,endIndex2))
}
if (!cache.has(key3)){
cache.set(key3,dfs(endIndex1-1,endIndex2-1))
}
return Math.min(cache.get(key1),cache.get(key2),cache.get(key3))+1
}
}
return dfs(len1-1,len2-1)
};动态规划
js
var minDistance = function(word1, word2) {
let len1=word1.length
let len2=word2.length
// 二维数组，第一个是行，第二个是列
let dp=new Array(len1+1).fill(0).map(()=>new Array(len2+1).fill(0))
// 补上边界数据
dp[0][0]=0 // word1、word2都为空字符
for (let i=1;i<=len1;i++){
dp[i][0]=i // word2为空字符，word1有几位就操作几次删除
}
for (let j=1;j<=len2;j++){
dp[0][j]=j // word1为空字符，word2有几位就操作几次删除
}
for (let i=1;i<=len1;i++){ // 行
for (let j=1;j<=len2;j++){ // 列
// 这两个索引，代表位置word1的i个字符、word2的j个字符
// 所以，for循环的不是索引，而是序数位置
if (word1[i-1]===word2[j-1]){
dp[i][j]=dp[i-1][j-1]
// 当i=1，j=1。 dp[0][j]、dp[i][0] 表示word1、word2位置为0的位置，也就是空字符串
// 因为有空字符串的情况，所以这也是for循环从1开始的原因
}else {
dp[i][j]=Math.min(dp[i][j-1],dp[i-1][j],dp[i-1][j-1])+1
}
}
}
// console.log(dp)
return dp[len1][len2]
};300. 最长递增子序列
递归，从枚举结果的角度
js
// --------- 递归超时
var lengthOfLIS = function(nums) {
function dfs(i){
// 最后一层
if (i===0){
return 1
}
// 其余层，从枚举结果的角度
let max=0
for (let j=0;j<i;j++){ // [x,x,x,j,x,x,i] i之前的每一个都可能是其递增子序列的上一个元素
if(nums[j]<nums[i]){
max=Math.max(max,dfs(j))
}
}
return max+1
}
// 枚举所有可能得结尾
let ans=0
for (let i=0;i<nums.length;i++){
ans=Math.max(ans,dfs(i))
}
return ans
};
// ---------记忆化搜索
var lengthOfLIS = function(nums) {
let cache=new Array(nums.length).fill(-1)
function dfs(i){
// 最后一层
if (i===0){
return 1
}
// 其余层，从枚举结果的角度
let max=0
for (let j=0;j<i;j++){
if(nums[j]<nums[i]){
if (cache[j]===-1){
cache[j]=dfs(j)
}
max=Math.max(max,cache[j])
}
}
return max+1
}
// 枚举所有可能得结尾
let ans=0
for (let i=0;i<nums.length;i++){
if (cache[i]===-1){
cache[i]=dfs(i)
}
ans=Math.max(ans,cache[i])
}
return ans
};改造为动态规划（dfs改成数组，递归改成循环）
js
var lengthOfLIS = function(nums) {
let dp=new Array(nums.length).fill(0)
for (let i=0;i<nums.length;i++){
for (let j=0;j<i;j++){
if(nums[j]<nums[i]){
dp[i]=Math.max(dp[i],dp[j])
}
}
dp[i]+=1
}
return Math.max(...dp)
};状态机DP
分成两类：不限交易次数、恰好/至少/至多交易k次
122. 买卖股票的最佳时机 II
分析
从枚举结果的角度看，第i天共有四种情况：
- i天持有股票
- i-1天卖出，i天买入
- i-1天持有，i天继续持有
- i天未持有股票
- i-1天卖出，i天仍然不买
- i-1天持有，i天卖出
递归边界不采用图中的（理解成本比较高），我们直接让i=0作为边界，即第1天
第一天持有收益是-prices[0]，第一天不持有收益是0
js
// --------- 回溯，会超时
var maxProfit = function(prices) {
// 递归从枚举结果角度，枚举第i天卖出(i从0开始)
// false表示该天不持有股票，true表示持有股票
// 每层返回值是利润
function dfs(i,hold){
// 最后一层
if (i===0){
return hold?-prices[0]:0
}
// 其余层（互斥的两种情况）
if (hold){
// 第i天持有
return Math.max(dfs(i-1,true),dfs(i-1,false)-prices[i])
}else {
//不持有
return Math.max(dfs(i-1,false),dfs(i-1,true)+prices[i])
}
}
return dfs(prices.length-1,false) // 最后一天一定是卖出的，所以这里是false
};
// --------- 记忆化
var maxProfit = function(prices) {
let cache=new Array(prices.length).fill(-1).map(()=>new Array(2).fill(-1))
function dfs(i,hold){
// 最后一层
if (i===0){
return hold?-prices[0]:0
}
// 其余层（互斥的两种情况）
// 记忆化（0对应false，1对应true）
if (cache[i-1][0]===-1){
cache[i-1][0]=dfs(i-1,0)
}
if (cache[i-1][1]===-1){
cache[i-1][1]=dfs(i-1,1)
}
if (hold){
// 第i天持有
return Math.max(cache[i-1][1],cache[i-1][0]-prices[i])
}else {
//不持有
return Math.max(cache[i-1][0],cache[i-1][1]+prices[i])
}
}
return dfs(prices.length-1,0) // 最后一天一定是卖出的，所以这里是false
};动态规划
递归改动态规划，有一点需要注意：关于for循环索引含义、递推公式中dp索引含义
例子
// 递归中 第i天持有股票
dfs(i,true)=Math.max(dfs(i-1,true),dfs(i-1,false)-prices[i])
// 换成dp 第i天持有股票
// 直接一对一转换是错的，注意 i=0时，dp[i-1]就是dp[-1]明显越界了
let dp=new Array(prices.length).fill(-1).map(()=>new
for (let i=0;i<prices.length;i++){
dp[i][1]= Math.max(dp[i-1][1],dp[i-1][0]-prices[i])
}
// 我们统一口径。i是索引，对应第i+1天。即price[0] 是第1天
// for循环需要从1开始
let dp=new Array(prices.length).fill(-1).map(()=>new
// 补上边界数据
dp[0][1]=-prices[0]
dp[0][0]=0
for (let i=1;i<prices.length;i++){
dp[i][1]= Math.max(dp[i-1][1],dp[i-1][0]-prices[i])
}js
var maxProfit = function(prices) {
// 二维数组，第一个是行，第二个是列
let dp=new Array(prices.length).fill(-1).map(()=>new Array(2).fill(-1))
// 补上边界数据
dp[0][1]=-prices[0]
dp[0][0]=0
for (let i=1;i<prices.length;i++){
dp[i][1]= Math.max(dp[i-1][1],dp[i-1][0]-prices[i])
dp[i][0]= Math.max(dp[i-1][0],dp[i-1][1]+prices[i])
}
return dp[prices.length-1][0] // 最后一天，一定要卖出
};动态数组降维优化
整个递归公式仅仅涉及 i 与 i+1 两个状态点，我们可以用两个存储。不必使用一个数组的空间去存储
js
var maxProfit = function(prices) {
// 二维数组，第一个是行，第二个是列
let dp=new Array(prices.length).fill(-1).map(()=>new Array(2).fill(-1))
// 补上边界数据
f1=-prices[0]
f0=0
for (let i=1;i<prices.length;i++){
[f0,f1]=[Math.max(f0,f1+prices[i]),Math.max(f1,f0-prices[i])]
}
return f0// 最后一天，一定要卖出
};309. 买卖股票的最佳时机含冷冻期
递归解法
js
// --------- 超时
var maxProfit = function(prices) {
function dfs(i,hold){
// 最后一层
if (i===0){
return hold?-prices[0]:0
}
// 其余层
if(hold){
return Math.max(dfs(i-1,true),dfs(i-2,false)-prices[i]) // 注意冻结期为1天，即第i-1天不能卖出，所以i-1与i-2是相同的。同时由于只能交易完成才能进行下一笔交易【1】i-1如果持有，则i-2一定也是持有的，无需考虑 【2】i-1如果持有，则i-2需要保证未持有，即递推式：dfs(i-2,false)-prices[i]
}else{
return Math.max(dfs(i-1,false),dfs(i-1,true)+prices[i])
}
}
return dfs(prices.length-1,false)
};
// --------- 记忆化动态规划
转动态规划时，由于存在dp[i-2]，所以i改为从2来开始
当i=2时，dp[i-2]就是dp[0]，这里就计算了第一天的状态，所以不用担心丢失
js
var maxProfit = function(prices) {
if(prices.length<=1){
return 0
}
dp=new Array(prices.length).fill(0).map(()=>new Array(2).fill(0))
dp[0][0]=0
dp[0][1]=-prices[0]
dp[1][0]=Math.max(0,-prices[0]+prices[1])
dp[1][1]=Math.max(-prices[0],-prices[1])
for (let i=2;i<prices.length;i++){
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1]=Math.max(dp[i-1][1],dp[i-2][0]-prices[i])
}
return dp[prices.length-1][0]
};188. 买卖股票的最佳时机 IV（最多k次交易）
分析
还是四种状态，但是这里多个一个变量j记录交易次数
只有在最后一天卖出，才会是最大收益，所以（买入-卖出）一定是成对存在的，这一对算是一笔交易，注意图中 卖出、买入，只要保证一个是j，另一个是j-1就行
图中时将买入记为一次交易
递归
js
// 会超时，可以改为记忆化
var maxProfit = function(k, prices) {
function dfs(i,j,hold){
// 最后一层
if (j===0){
return 0
}
if (i===0){
return hold?-prices[0]:0
}
// 其余层
if (hold){ // 第i+1天是否持有
return Math.max(dfs(i-1,j,true),dfs(i-1,j-1,false)-prices[i]) // dfs(i-1,j-1,false)-prices[i] 是买入，记为一次交易
}else {
return Math.max(dfs(i-1,j,false),dfs(i-1,j,true)+prices[i])
}
}
return dfs(prices.length-1,k,0)
};动态规划
上一题提到了统一for循环变量的含义，这个题有个特殊点 交易存在0次的概念，从0到k次，这是k+1个数，需要用k+1长度的数组来存储
js
var maxProfit = function(k, prices) {
// 三维数组，for循环时按照创建的顺序遍历。例如这里先创建了prices.length的数组，for循序先循序prices.length
const dp=new Array(prices.length).fill(0).map(()=>new Array(k+1).fill(0).map(()=>new Array(2).fill(0))) // 这里是k+1
// dp[0][1][1]=-prices[0]
// dp[0][0][0]=0
// dp[0][1][0]=0
for (let j = 1; j <= k; j++) {
dp[0][j][1] = -prices[0];
}
for (let i=1;i<prices.length;i++){ // i表示i+1天（正常情况）
for (let j=1;j<=k;j++){ // k表示k次交易。因为交易是有0-k，共k+1个情况。注意这里是 <=k
dp[i][j][1]=Math.max(dp[i-1][j][1],dp[i-1][j-1][0]-prices[i])
dp[i][j][0]=Math.max(dp[i-1][j][0],dp[i-1][j][1]+prices[i])
}
}
return dp[prices.length-1][k][0] // 注意这里最后一位是 [k]，不是[k-1]
};动态规划降维，暂时跳过
区间dp
线性dp一般是在 前缀、后缀上转移（dp[i] 与 dp[i-1]、dp[i-2]之间转移），而区间dp是从小区间转化为大区间
1039. 多边形三角剖分的最低得分
题目
js
//你有一个凸的
// n 边形，其每个顶点都有一个整数值。给定一个整数数组
// values ，其中
// values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。
//
// 假设将多边形 剖分 为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之
//和。
//
// 返回 多边形进行三角剖分后可以得到的最低分k从i点开始，顺时针遍历
递归解法
js
// 超时
var minScoreTriangulation = function(values) {
function dfs(i,j){
// 最后一层
if (i+1===j){
return 0 // 只有两个点，无法组成三角形
}
let minScore=Infinity
// 其余层
for (let k=i+1;k<=j-1;k++){ // 这个for循环一直在缩小区间
minScore= Math.min(minScore,dfs(i,k)+dfs(k,j)+values[i]*values[j]*values[k])
}
return minScore
}
return dfs(0,values.length-1)
};
// 记忆化
var minScoreTriangulation = function(values) {
const cacheMap={}
function dfs(i,j){
// 最后一层
if (i+1===j){
return 0
}
let minScore=Infinity
// 其余层
for (let k=i+1;k<=j-1;k++){
if (!cacheMap[`${i},${k}`]){
cacheMap[`${i},${k}`]=dfs(i,k)
}
if (!cacheMap[`${k},${j}`]){
cacheMap[`${k},${j}`]=dfs(k,j)
}
minScore= Math.min(minScore,cacheMap[`${i},${k}`]+cacheMap[`${k},${j}`]+values[i]*values[j]*values[k])
}
cacheMap[`${i},${j}`]=minScore
return minScore
}
return dfs(0,values.length-1)
};动态规划
区间dp类问题，从递归改成循环时，注意遍历顺序
解释下循环顺序：
必须让递推是能一步一步推过来，上一步的dp值必须有了，才能退出下一步的dp，所以，必须有顺序
目标求dp[i][j]，根据递推公式必须先有 dp[i][k]、 dp[k][j]
简单记：从大的推来的，倒序；从小的推来的，正序；
而i<k<j关系原因见下图：
动态规划
js
function minScoreTriangulation(values) {
let n= values.length
let dp=new Array(n).fill(0).map(()=>new Array(n).fill(0))
// i<k<j
for (let i=n-2;i>=0;i--){ // 下面递推公式初始k=i+1，我们必须保证value[k]、dp[i][k]、dp[k][j]其中的k有意义
for (let j=i+2;j<n;j++){ // j是三角形右边界，所以一定比i大2
let maxCount=Infinity
for(let k=i+1;k<j;k++){
maxCount=Math.min(maxCount,Math.min(dp[i][k]+dp[k][j]+values[i]*values[j]*values[k]))
}
dp[i][j]=maxCount
}
}
return dp[0][n - 1];
}516. 最长回文子序列
求得子序列就是子集，很容易想到选、不选的回溯解法。但是超时！！！
js
// 由于不是将结果return到顶层，所以不能用记忆化
var longestPalindromeSubseq = function(s) {
let maxCount=0
function dfs(startIndex,path){
//
if(startIndex===s.length){
if(path.join('')===path.slice().reverse().join('')){
maxCount = Math.max(maxCount,path.length)
}
return
}
// 不选
dfs(startIndex+1,path)
// 选
path.push(s[startIndex])
dfs(startIndex+1,path)
path.pop()
}
dfs(0,[])
return maxCount
};
// 可以记忆化区间动态规划（猜想子集型回溯都能，这种方式解，还未验证）
- i是左指针、j是右指针。分别指向字符串的左右两侧
- 当左右指针指向的字符一样时，则回文子串长度+2
- 不一样，则看下左、右哪个回文子串长度大，选那个
- i==j，只有一个字符即回文长度为1
js
var longestPalindromeSubseq = function(s) {
const n=s.length
const dp=new Array(n).fill(0).map(()=>new Array(n).fill(0))
// 将边界带入递推公式，需要下面边界
// dp[n-1][n-2] // i是左边界、j是右边界，这种情况是没有实际含义的，回文子串长度为0
// dp[n-1][n-1]、dp[n-2][n-2] // 循环初始化
for (let i = 0; i < s.length; i++) {
dp[i][i] = 1;
}
for (let i=n-2;i>=0;i--){
for (let j=i+1;j<n;j++){
if(s[i]===s[j]){
dp[i][j]= dp[i+1][j-1]+2
}else{
dp[i][j]= Math.max(dp[i+1][j],dp[i][j-1])
}
}
}
return dp[0][n-1]
};树形dp
路径
543. 二叉树的直径
分析：最长直径一定是包含拐点的
这个题有个特征，二叉树的递归并不是答案，递归仅仅是计算节点深度的
但是，我们在这个递归中不断更新答案ans
js
var diameterOfBinaryTree = function(root) {
// 一定过拐点
let max=0
function dfs(node){
// 最后一层
if(node===null){
return 0
}
// 其余层
const leftDepth=dfs(node.left)
const rightDepth=dfs(node.right)
// return 的是每层的最大深度 ，深度-1，才是直径（边数）
// leftDepth+rightDepth=left直径+right直径+2 这是对的
max=Math.max(max,leftDepth+rightDepth)
return Math.max(leftDepth,rightDepth)+1
}
dfs(root)
return max
};124. 二叉树中的最大路径和
上一题直径是边数之和，这题路径和是节点val之和
上一题直径是边数肯定是正数，即越大越好；这题路径节点val可能是负数
解
js
var maxPathSum = function(root) {
let ans=-Infinity
function dfs(node){
if (node===null){
return 0
}
let left=dfs(node.left)
let right=dfs(node.right)
// 答案
ans=Math.max(ans,left+right+node.val)
// 递归 ，这里的关键是0
// 下面二叉树， 最长路径的起始一定得是正数，也就是不能从-2开始，而是4开始
//
// 0
// / \
// -1 2
// / \
// 3 4
// /
// -2
return Math.max(0,Math.max(left,right)+node.val)
}
dfs(root)
return ans
};2246. 相邻字符不同的最长路径
最大独立集
337. 打家劫舍 III
情况：
- 根节点选，左右孩子不能选
- 根节点不选，左右孩子都选（都选才能最大）
错误解法
js
var rob = function(root) {
function dfs(node){
// 最后一层
if(node===null){
return 0
}
// 其余层
let left=dfs(node.left)
let right=dfs(node.right)
// 错误点：这里丢掉了一层关系啊。选当其节点，必定是左（右）子树中的根节点不选，否则就相连了
return Math.max(left+right,node.val+left,node.val+right)
}
return dfs(root)
};解
js
var rob = function(root) {
function dfs(node){
// 最后一层
if(node===null){
return [0,0]
}
// 其余层
let [leftSelectRoot,leftNoSelectRoot]=dfs(node.left)
let [rightSelectRoot,rightNoSelectRoot]=dfs(node.right)
// 选当前。不选左右孩子的根节点
let selectRoot=node.val+leftNoSelectRoot+rightNoSelectRoot
// 不选当前。选左右孩子 。这里有个点：左（右）子树的根选与不选，需要比较哪个大
let noSelectRoot=Math.max(leftSelectRoot,leftNoSelectRoot)+Math.max(rightSelectRoot,rightNoSelectRoot)
return [selectRoot,noSelectRoot]
}
return Math.max(...dfs(root))
};
树上最小支配集
968. 监控二叉树
js
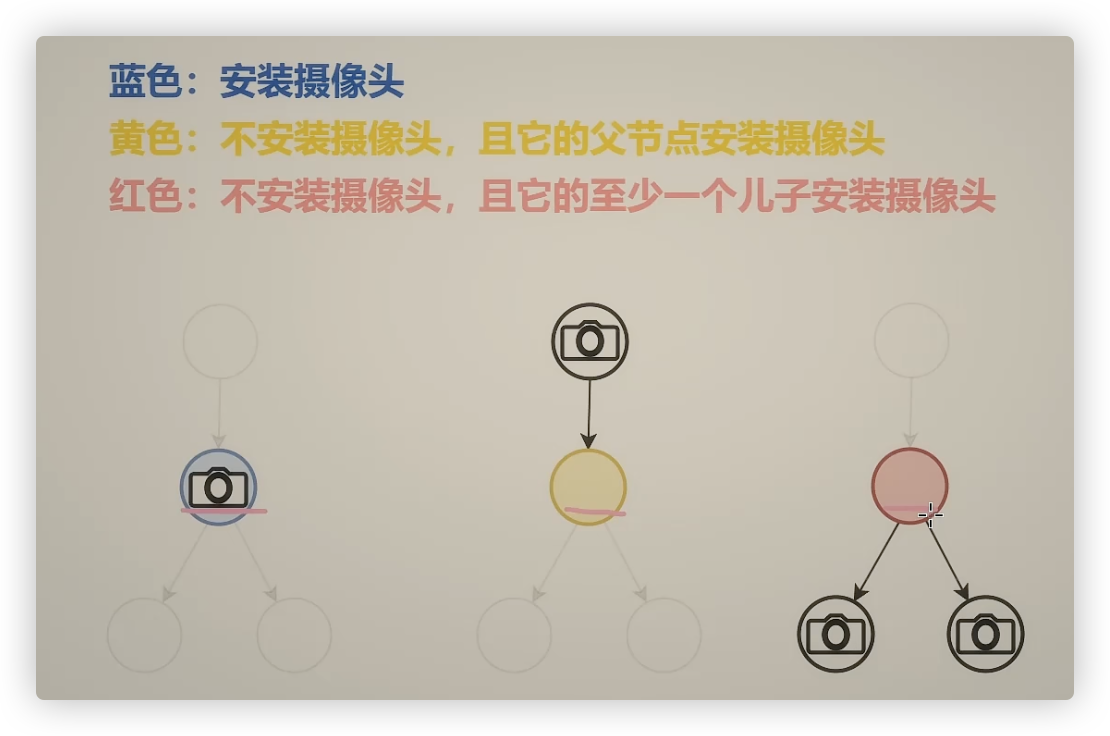
var minCameraCover = function(root) {
function dfs(node){
// 最后一层
if (node==null){
return [Infinity,1,0] // Infinity表示无意义，这题求最小值，所以是正无穷
}
// 其余层
const [l_by_self,l_by_father,l_by_children]= dfs(node.left)
const [r_by_self,r_by_father,r_by_children]= dfs(node.right)
// 仅当前节点装监控（左节点、左节父节点、左节点孩子）
let self=Math.min(l_by_self,l_by_father,l_by_children)+Math.min(r_by_self,r_by_father,r_by_children)+1
// 仅当前节点的父结点装监控（左节点，左节子节点。当其节点就是左子节点父节点，已明确不安装监控）
let father=Math.min(l_by_self,l_by_children)+Math.min(r_by_self,r_by_children)
// 仅当前节点的孩子结点装监控（哪个孩子节点安装？即左、右、左+右）
let children=Math.min(l_by_self+r_by_children,l_by_children+r_by_self,l_by_self+r_by_self)
return [self,father,children]
}
const [self,,children]=dfs(root) // 根节点
return Math.min(self,children)
};
js
仅当前节点装监控这步
+1 改成 cost[node]二叉树
dfs（递归）
104. 二叉树的最大深度
return通讯，将结果返回顶层
js
var maxDepth = function(root) {// 0 层
// 最后一层 （root -> root.left、root.right，一步步下移为null）
if(root===null){
return 0
}
// 其它层（假设是1层）
// maxDepth(root.left)\maxDepth(root.right)是第2层
// 这里计算的是1层的结果
const latter=Math.max(maxDepth(root.left),maxDepth(root.right)) // n+1层结果做逻辑处理。这里是取最大值
return 1+latter
};参数通讯
注意：
leetcode给的模板
var maxDepth = function(root){}，如果使用maxDepth作为递归函数，那就没法自定义每层的参数。所以，我们可以在自定义一个全新的递归函数参数想下传递最后无法取出，所以我们一般定义个全局的变量去收集每层的数据
js
var maxDepth = function(root) {
let ans=0
function recursion(root,count){
// 最后一层
if(root===null){
return 0
}
// 其余层
count++
ans=Math.max(count,ans)
recursion(root.left,count)
recursion(root.right,count)
}
recursion(root,0)
return ans
};111. 二叉树的最小深度
这个题很容易做错，直接把上一题的取左右子树最大的，改成取左右子树最小的
Math.min(minDepth(root.left),minDepth(root.right))可以看下面的例子，因为把并不存在的右子树算上了，右子树不存在但是被错误的认为其最小高度为0，导致计算错误
js
var minDepth = function(root) {
function dfs(node){
//
if (node===null) {
return 0
}
//
if(node.left&&node.right===null){
return dfs(node.left)+1
}
if (node.left===null&&node.right){
return dfs(node.right)+1
}
return Math.min(dfs(node.left),dfs(node.right))+1
}
return dfs(root)
};100. 相同的树
js
var isSameTree = function(p, q) {
function dfs(p,q){
// 最后一层
if (p===null||q===null){
if (p===q){
return true
}else {
return false
}
}
// 其余层
if(dfs(p.left,q.left)&&dfs(p.right,q.right)&&p.val===q.val){
return true
}else {
return false
}
}
return dfs(p,q)
};101. 对称二叉树
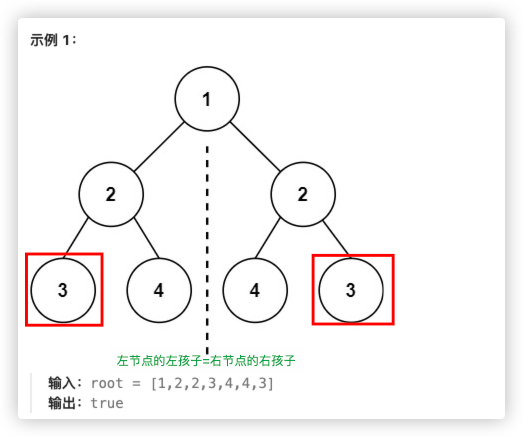
与上个题一样的，是中轴对称所以把根节点的左右子树传入，且
- 左节点的左孩子=右节点的右孩子
- 左节点的右孩子=右节点的左孩子
js
var isSymmetric = function(root) {
function dfs(leftNode,rightNode){
// 最后一层
if (leftNode===null||rightNode===null){
return leftNode===null&&rightNode===null
}
// 其余层
if (leftNode.val===rightNode.val&&dfs(leftNode.left,rightNode.right)&&dfs(leftNode.right,rightNode.left)){
return true
}
return false
}
return dfs(root.left,root.right)
};226. 翻转二叉树
js
var invertTree = function(root) {
if (root===null){
return null
}
let left=invertTree(root.left)
let right=invertTree(root.right)
root.left=right
root.right=left
return root
};
// 2刷时的一种错误写法
var invertTree = function(root) {
if (root===null){
return null
}
root.right=invertTree(root.left)
// 下面这里的root.right已经不是原来的右子树了，而是上一步翻转后的右子树了，所以这样写错误
root.left=invertTree(root.right)
return root
};js
var invertTree = function(root) {
// 最后一层
if (root===null){
return null
}
// 其余层的处理逻辑
let temp=root.left
root.left=root.right
root.right=temp
// 递归到下一层，下一层也是其余层处理逻辑
invertTree(root.left)
invertTree(root.right)
return root
};112. 路径总和（叶子节点类型总结）
最近的几道题总是遇到叶子节点的问题
1
/ \
2 3
/
4
上面的节点3，他本身不是叶子节点，但是他的右节点是null
我们常用的递归终点都是 if(node===null){ xxx } ，如果题目求的是类似根节点到叶子节点路径的问题，很容易将3作为叶子节点误判
叶子节点边界：
if(node.left===null&&node.right===null)
由于3这种节点的存在，递归过程过程中使用左右节点都要判断（过去使用node===null作为边界，不用判断，就算node.left是null，进入dfs(node.left)也会被边界拦住）
if(node.left){
dfs(node.left)
}
if(node.right){
dfs(node.right)
}js
var hasPathSum = function(root, targetSum) {
if (root===null){ // 输入用例：[]，输出false
return false
}
let ans=false
function dfs(node,sum){
// 注意：上部分讲解中节点3，就不是叶子节点
if (node.left===null&&node.right===null){
if(sum+node.val===targetSum){
ans=true
}
return
}
//
if (node.left){
dfs(node.left,sum+node.val)
}
if (node.right){
dfs(node.right,sum+node.val)
}
}
dfs(root,0)
return ans
};437. 路径总和 III
这道题写了两遍递归，挺少见的
rootSum(node,sum) 是以node作为根节点，递归找出的符合条件的路径。这也是常写的递归，以前没有注意到，dfs是从固定节点开始的递归
dfs(node)是递归数，把全部节点作为根节点传入rootSum
js
var pathSum = function(root, targetSum) {
let count=0
function dfs(node){
//
if (node===null){
return
}
//
rootSum(node,0)
dfs(node.left)
dfs(node.right)
}
function rootSum(node,sum){
//
if (node===null){
return
}
sum+=node.val
if (sum===targetSum){ // 这里已经和为targetSum为什么不return。因为节点值可能是负值
count++
}
// 选左
rootSum(node.left,sum)
// 选右
rootSum(node.right,sum)
sum-=node.val
}
dfs(root)
return count
};257. 二叉树的所有路径
这个题常规思路，从选当前节点的左、右，分出两种可能
有一点需要注意，写的时候很犹豫，path.pop的位置在哪里？
注意：选左孩子、右孩子是互斥的不会同时发生，所以只会执行一个pop
js
var binaryTreePaths = function(root) {
// 子集型回溯
let ans=[]
function dfs(node,path){
// 最后一层
if (node.left===null&&node.right===null){
// 注意：叶子节点记得推
path.push(node.val)
ans.push(path.join('->'))
return
}
// 其余层，当前层n
path.push(node.val)
// n+1层选左
if (node.left){
dfs(node.left,path)
path.pop()
}
// n+1层选右
if (node.right){
dfs(node.right,path)
path.pop()
}
}
dfs(root,[]) // 通过数组收集每一条路径
return ans
};110. 平衡二叉树
平衡二叉树：所有节点左右子树深度只差小于等于1
一直递归返回深度，但是在递归过程中计算是否平衡。
这是一种思路：保持递归，用额外变量存储题目的解。非常常见的就是利用利用深度
js
var isBalanced = function(root) {
let isBalancedStatus=true
function dfs(node){
// 最后一层
if (node===null){
return 0
}
if (isBalancedStatus){
isBalancedStatus=Math.abs(dfs(node.left)-dfs(node.right))<=1
}
// 其余
return Math.max(dfs(node.left),dfs(node.right))+1
}
dfs(root)
return isBalancedStatus
};199. 二叉树的右视图
这题还是利用深度递归，只不过我们是从上向下传入深度的
主要是因为这个题的思路：
从图可以看到最后的结果不一定都是右子树，我们利用深度递归，优先递归右子树并放入数组（深度是索引），如果深度d存过了，就不再存了。这样就能保证每层都存第一个
js
var rightSideView = function(root) {
let res=[]
function dfs(node,depth){
// 最后一层
if (node===null){
return
}
// 其余层
if(res[depth]===undefined){
res[depth]=node.val
}
dfs(node.right,depth+1)
dfs(node.left,depth+1)
}
dfs(root,0)
return res
};236. 二叉树的最近公共祖先
当前节点p或q，则当前节点就是公共父节点
只有当前节点，左右子树分别含有p、q，当前节点才是公共父节点
这题和常规的递归有些不同。if判断不是边界，而是找到目标，每层向上返回的最终结果是节点
js
var lowestCommonAncestor = function (root, p, q) {
function dfs(node) {
// 最后一层。 要是到树的叶子节点了，要么是找到p、q了，就停止
if (node === null||node === p || node === q) {
return node
}
// 其余层
const left = dfs(node.left)
const right = dfs(node.right)
// 找到p、q
if (left && right) {
return node
}
if (left) {
return left
}
if (right) {
return right
}
return null
}
return dfs(root)
};235. 二叉搜索树的最近公共祖先
上一题的代码在这里也能用
与上一题不同点在于二叉搜索树。其特性为 ：任意节点右子树所有节点大于其本身，左子树所有节点小于其本身。我们可以利用这个特性优化
形式仍然与传统的递归不一样，这里是因为return root，隐含了root是null的情况
js
var lowestCommonAncestor = function(root, p, q) {
if (p.val<root.val&&q.val<root.val){
return lowestCommonAncestor(root.left,p,q)
}
if (p.val>root.val&&q.val>root.val){
return lowestCommonAncestor(root.right,p,q)
}
// 这里就是p、q分别在左右子树上。由于递归是从底层向上返回的，第一个一定是最近公共子父节点
return root
};114. 二叉树展开为链表
in-place 的意思可能更多说的是直接在原来的节点上改变指向，空间复杂度并没有要求
注意：如果先序遍历生成数组后，在根据数组创建结果是错的，因为没有在原root上更改。即使下面这样最后赋值给root也是错误的，因为root原指向对象没有变化
js
// 【错误解法！！！！】
var flatten = function(root) {
const ansRoot=new TreeNode(null)
function dfs(node){
if(node===null){
return
}
ansRoot.left=null
ansRoot.right=new TreeNode(node.val)
dfs(node.left)
dfs(node.right)
}
dfs(root)
root = ansRoot
return root
};前、中、后序遍历
本质仍然是dfs。下面的都是从上到下通过数组收集结果
98. 验证二叉搜索树（中序）
二叉搜索树：任意节点右子树所有节点大于其本身，左子树所有节点小于其本身
8
/ \
4 10
/ \
3 5遍历树的方式：前序、中序、后序，每种遍历方式都有其独特的特性和应用场景：
js
前序遍历（Preorder Traversal）：
特性：访问顺序为根节点 -> 左子树 -> 右子树（VLR）。
应用：前序遍历常用于复制一颗二叉树或构造表达式树，因为操作（如打印、计算表达式）先于访问子树，适用于需要优先处理根节点的场景。它也是许多算法和数据结构的基础，比如编译原理中的语法分析、哈夫曼编 码树的构建等
中序遍历（Inorder Traversal）：
特性：访问顺序为左子树 -> 根节点 -> 右子树（LVR）。
应用：中序遍历在二叉搜索树（BST）中特别有用，它可以保证遍历的结果是升序的，因此常用于对二叉搜索树进行排序和查找操作。此外，它也适用于需要中间节点值参与决策的算法中，比如符号表的实现。
后序遍历（Postorder Traversal）：
特性：访问顺序为左子树 -> 右子树 -> 根节点（LRV）。
应用：后序遍历适用于那些需要先处理子节点再处理父节点的场景，例如计算表达式的逆波兰表示（Reverse Polish Notation, RPN）、树的删除操作等。它在计算表达式树的值时特别有用，因为先计算子表达式再合并结果的逻辑与后序遍历的顺序相吻合。判断一棵树是否为二叉搜索树，可以利用中序遍历结果是升序的特性
中序遍历
c
var isValidBST = function(root) {
let path=[]
// 中序遍历
function inOrder(node){
if(node===null){
return
}
inOrder(node.left)
path.push(node.val)
inOrder(node.right)
}
inOrder(root)
let res=true
path.reduce((pre,cur)=>{
if(pre>=cur){
res=false
}
return cur
})
return res
};在中序遍历的过程中做比较(这种比较难理解，需要一直记录上一个元素)
2刷：一直比较node.val与node.left.val 、node.val与node.right.val的关系来判断是不是搜索二叉树，这是典型的错误。二叉树：任意节点的右孩子>左子树任意节点的值
注意：下面这个树任意节点都是 当前节点>左子树、当前节点<右子树，但是整体来看不满足定义，节点7已经大于了节点5
真正比较的是中序遍历结果数组的前一个
js
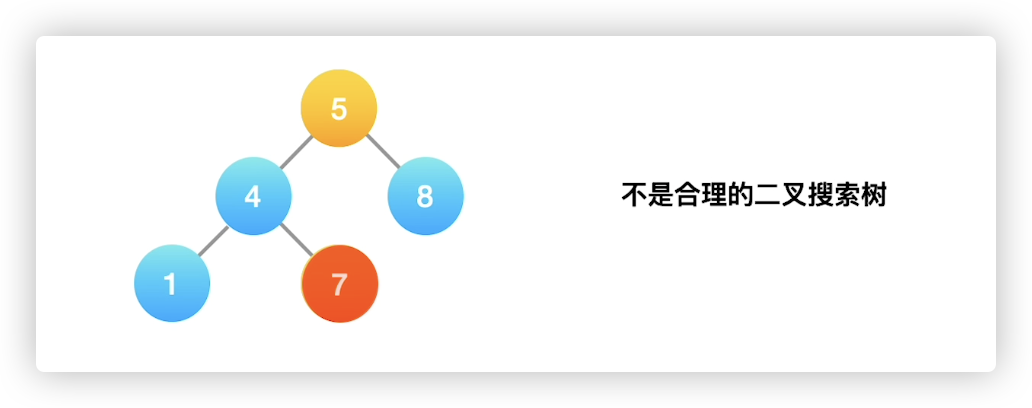
var isValidBST = function(root) {
//
let pre=-Infinity
function dfs(node){
// 最后一层
if(node===null){
return true
}
// 其余
let isLeftBST= dfs(node.left)
if (!isLeftBST||pre>=node.val){
return false
}
pre=node.val
return dfs(node.right)
}
return dfs(root)
};230. 二叉搜索树中第 K 小的元素（中序）
简单思路就是中序遍历，遍历的结果是从小到大的，题目要求取第K小的元素，就是变量结果的K-1号元素
js
var kthSmallest = function(root, k) {
const inOrderList=[]
function dfs(node){
// 最后一层
if(node===null){
return
}
// 其余层
dfs(node.left)
inOrderList.push(node.val)
dfs(node.right)
}
dfs(root)
return inOrderList[k-1]
};与98题类似，我们可以在递归过程中，一直进行比较找打第K小的元素。但是递归是无法终止的，即使找到了也会一直递归整棵树。所以，我们可是使用迭代的形式
144. 二叉树的前序遍历
js
var preorderTraversal = function(root) {
let ans=[]
function preOrder(node){
if (node===null){
return
}
ans.push(node.val)
preOrder(node.left)
preOrder(node.right)
}
preOrder(root)
return ans
};94. 二叉树的中序遍历
var inorderTraversal = function(root) {
let ans=[]
function preOrder(node){
if (node===null){
return
}
preOrder(node.left)
ans.push(node.val)
preOrder(node.right)
}
preOrder(root)
return ans
};层次遍历（bfs）
bfs广度优先，在树的范畴内就是层次遍历
推荐记忆102题层次遍历的代码作为模版。while...for的方式
102. 二叉树的层序遍历
层次遍历实现
js
var levelOrder = function(root) {
let queue=[root]
let ans=[]
while (queue.length!==0){
const node=queue.shift()
ans.push(node.val)
if (node.left){
queue.push(node.left)
}
if (node.right){
queue.push(node.right)
}
}
return ans
};本题重点是
答案是：[[3],[9,20],[15,7]]
层次遍历的结果：[ 3, 9, 20, 15, 7 ]
正确答案每层都在一个数组内解法1：bfs思路
js
var levelOrder = function(root) {
if (root===null){
return []
}
let queue=[root]
let ans=[]
while (queue.length!==0){ // 当前层元素个数
ans.push([])
const len= queue.length // 注意：开始的时候for循环直接使用queue.length。但是for循环过程中queue长度在变换，所以这里必须要存下长度
for (let i=0;i<len;i++){ // for循环把本层的数据出队处理完
const node=queue.shift()
ans[ans.length-1].push(node.val)
// 在queue继续追加子元素，但是for循环只读完了本层。
if (node.left){
queue.push(node.left)
}
if (node.right){
queue.push(node.right)
}
}
}
return ans
};解法2：dfs思路。这个思路遇到过好几次，利用树的深度递归。在递归过程中收集答案
js
var levelOrder = function(root) {
let ans=[]
function dfs(node,depth){
// 最后一层
if(node===null){
return
}
// 其余任意层n
// 不使用return传递数据，而是从上到下。两个dfs是指导第n+1层的逻辑，本层逻辑只有下面一段
if(!ans[depth]){
ans[depth]=[]
}
ans[depth].push(node.val)
// 这里需要保持左递归、右递归。才能是一层从左到右排列
dfs(node.left,depth+1)
dfs(node.right,depth+1)
}
dfs(root,0)
return ans
};107. 二叉树的层序遍历 II
与上题一致的地方是，返回的值还是子数组构成的大数组。返回值就是上一题结果反过来
解法1：是把上题的dfs、bfs的结果 reverse 后返回
解法2：
js
ans[depth].push(node.val)
改为
ans[depth].unshift(node.val)297. 二叉树的序列化与反序列化
注意，根据层次遍历结果是无法还原原来的树的
1
/ \
2 3
/ \
4 5
1
/ \
2 3
\ /
4 5
// 层次遍历结果都是: 1,2,3,4,5。无法确定原本的树
// 但是，我们可以改造层次遍历，以完全二叉树的形式存储 1,2,3,null,null,4,5 ，技能明确原来树结构但是serialize生成的字符串序列，把空白节点补全为null了
1
/ \
2 3
/ \
4 5
//serialize结果： 1,2,3,null,null,4,5,null,null
1
\
3
/ \
4 5
//serialize结果： 1,null,3,4,5,null,null 【特别注意：null节点的左右孩子就不补充null了】js
/**
* 序列化为完全二叉树的表示形式
*/
var serialize = function(root) {
if (root===null){
return ''
}
let ans=[]
let queue=[root]
while (queue.length!==0){
const len=queue.length
// 消费本层数据。queue会推入下一层数据，作为下一轮while循环使用
for (let i=0;i<len;i++){
const node = queue.shift()
// 注意2：下面注意1提示会推入null，这里shift出队的node就可能是null
if (node){
ans.push(node.val)
// 注意1：node如果是叶子节点，这里node.left、node.right就是null
queue.push(node.left)
queue.push(node.right)
}else {
// 如果是null，就不没有左右孩子了
ans.push(null)
}
}
}
return ans.join(',')
};
/**
* Decodes your encoded data to tree.
*
* @param {string} data
* @return {TreeNode}
*/
var deserialize = function(data) {
// 最后一个节点索引=Math.floor(最后一个节点索引/2)
// 父节点索引为i，左孩子=(2*i)+1
if (data===''){
return null
}
const list=data.split(',')
const root=new TreeNode(list.shift())
let queue=[root] // 这里也需要一个队列，是因为要一直存下一层的所有节点
while (list.length!==0){
const len=queue.length
for (let i=0;i<len;i++){
const node=queue.shift()
if (node){
let leftVal=list.shift()
if (leftVal){
let leftNode= new TreeNode(leftVal)
node.left=leftNode
queue.push(leftNode)
}
let rightVal=list.shift()
if (rightVal){
let rightNode=new TreeNode(rightVal)
node.right=rightNode
queue.push(rightNode)
}
}
}
}
return root
};构造树
根据数组构造二叉树
根据数组构造二叉搜索树：任意节点A，其右子树都小于A的值，左子树都大于A的值
注意：下面这个树任意节点都是 当前节点>左子树、当前节点<右子树，但是整体来看不满足定义，节点7已经大于了节点5
根据数组构造平衡树：任意节点的左右子树深度差<=1
根据 （前、中序）或者（中、后序）遍历结果构造树
108. 将有序数组转换为二叉搜索树
如果直接将一个普通数据构造为平衡树（平衡树也是二叉树搜索树的一种）十分的复杂，代码量估计超过100行
这个题可以利用有序数组的条件
js
var sortedArrayToBST = function(nums) {
function dfs(nums,left,right){
// 最后一层
if (left>right){ // left===right
return null
}
// 其余层
const mid=Math.floor((left+right)/2)
const node=new TreeNode(nums[mid])
node.left=dfs(nums,left,mid-1)
node.right=dfs(nums,mid+1,right)
return node
}
return dfs(nums,0,nums.length-1)
};补充：dfs、bfs
广度优先（BFS）
需要辅助队列
思想：从根节点开始寻找子节点，先遍历寻找兄弟节点，依次从上往下，按层级依次搜索
代码实现：根节点入队，之后出队节点x，会将其左右子节点入队，然后继续循环出队，入队子节点的流程，直到队列为空
模拟过程：
- 第一次入队根节点 1 【1】
- 1 出队，2、3入队 【2、3】
- 2 出队 ，4、5入队 【3、4、5】
- 3出队 ， 6、7入队 【4、5、6、7】
- 4出队，无子节点入队了
- 5出队
- 6出队
- 7出队
模板：
js
/**
* function ListNode(val) {
* this.val = val;
* this.left = null;
* this.right = null;
* }
*/
function bfs(root){
let queue=[root.val]
while(queue.length!==0){
// temp 不断遍历整个树
const temp=queue.shift()
if(temp.left){
queue.push(temp.left)
}
if(temp.right){
queue.push(temp.right)
}
}
}深度优先（DFS）
需要辅助栈（使用递归DFS函数的思路，可以不用辅助栈）
思想：从根开始，遇到一个节点，就先查询的它未被访问过的子节点，如果子节点还有未被访问过的子节点就继续往下寻找直到最后没有为止，再从根子节点的兄弟节点开始依次向下寻找节点
代码实现：根节点入栈，如果有子节点（优先入栈左孩子）就记录下下访问过后，继续入栈。直到没有子节点可以入栈了，就开始出栈每一个出栈的节点检查其是否还有未被访问过的孩子，如果有就录下访问过后，入栈该孩子节点，直到栈空结束
模拟过程：
- 1入栈 【1】
- 2入栈 【1、2】
- 4入栈 【1、2、4】
- 没有可以入栈的子节点了，4出栈 【1、2】
- 2出栈，2有右子节点，所以5入栈 【1、5】
- 出栈【1】
- 3入栈【1、3】
- 6入栈【1、3、6】
- 6出栈【1、3】
- 3出栈，3有右子节点，所以7入栈 【1、7】
- 7出栈
- 1出栈
模板：
js
/**
* function ListNode(val) {
* this.val = val;
* this.left = null;
* this.right = null;
* }
*/前缀树/字典树
节点除了存储字符，还要存储是否为单词结尾
单词no，到o节点就是终点了。对于单词nova到a节点才是终点
前缀树常用做搜索提示，Gin框架匹配路由也是使用前缀树实现的路由匹配
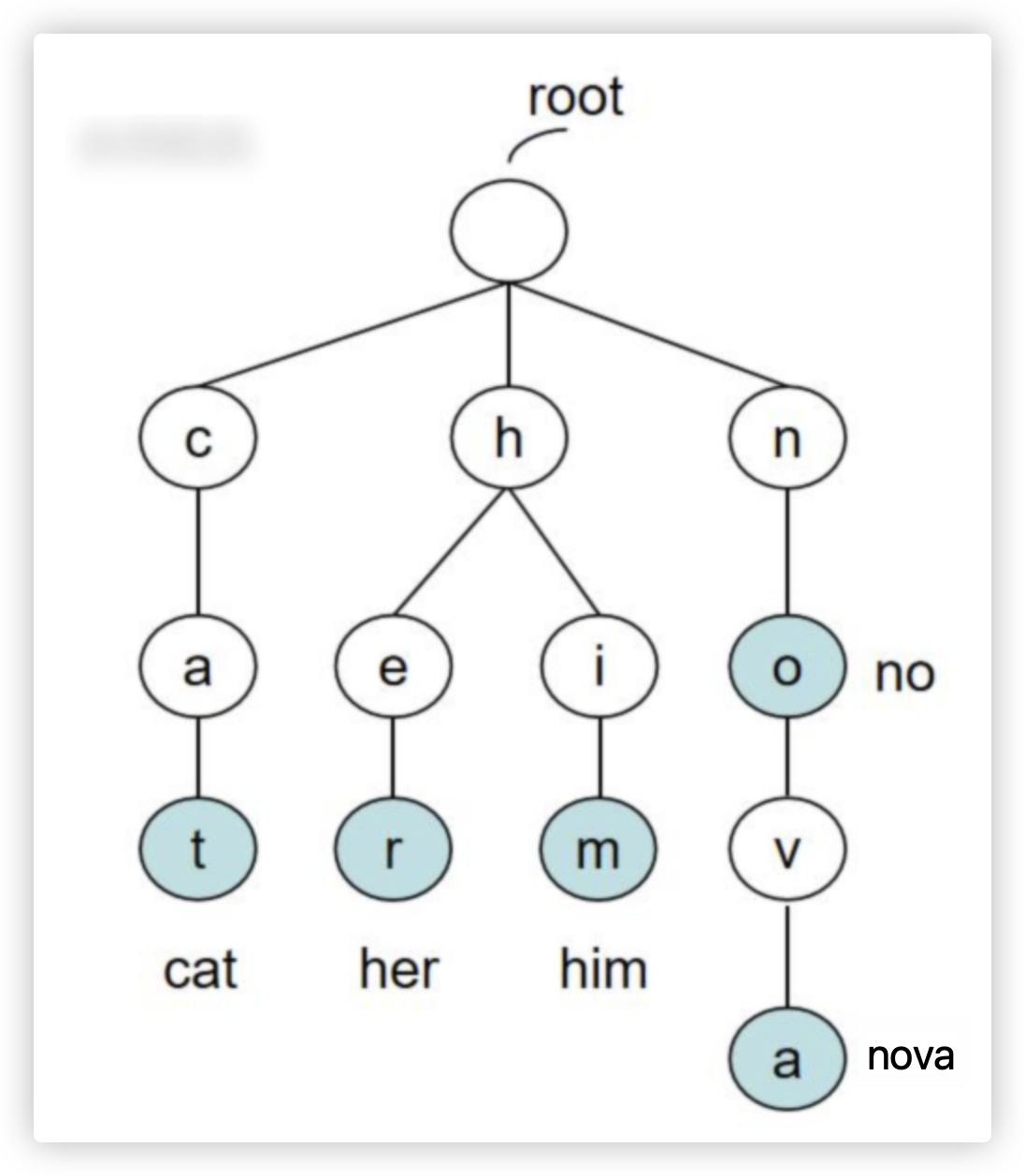
前缀树的节点结构并不是下面这种
function(val,isEnd){
this.val=val
this.children=[]
this.isEnd=isEnd
}而是，如何记录当前节点是多少？其实这里有一个隐含的逻辑
输入单词 a，我们从root节点的children找到a节
其中，a节点并没有记录自己的val是a，而是通过父节点得知
function(val){
this.children=[]
this.isEnd=isEnd
}208. 实现 Trie (前缀树)
JS实现版本
js
var Trie = function() {
this.children={}
};
/**
* @param {string} word
* @return {void}
*/
Trie.prototype.insert = function(word) {
let node=this.children // 当前节点的孩子
for (let ch of word){
if (!node[ch]){
node[ch]={}
}
node=node[ch] // 每次都移动到下一个节点
}
node.isEnd=true
};
/**
* @param {string} word
* @return {boolean}
*/
Trie.prototype.search = function(word) {
let node=this.children
for (let ch of word){
if (!node[ch]){
return false
}
node=node[ch]
}
return !!node.isEnd
};
/**
* @param {string} prefix
* @return {boolean}
*/
Trie.prototype.startsWith = function(prefix) {
let node=this.children
for (let ch of prefix){
if (!node[ch]){
return false
}
node=node[ch]
}
return true
};
// 测试
const root=new Trie()
root.insert('abc')
root.insert('abcd')
root.startsWith('ab')Go语言实现版本
go
// https://mp.weixin.qq.com/s/_4K-zDZgCPvSBmjHbj6GGA
package main
import "fmt"
type TrieNode struct {
//next [26]*TrieNode // 这个设计很精巧，没有存储单词的值，而是用索引表示。下一个找a，就去next[0]
next map[rune]*TrieNode
passCount int
end bool
}
type Trie struct {
root *TrieNode
}
func NewTrie() *Trie {
return &Trie{
root: &TrieNode{},
}
}
func (t *Trie) Insert(word string) {
move := t.root
for _, letter := range word {
if _, ok := move.next[letter]; !ok {
//没有,就直接插入
if move.next == nil {
move.next = make(map[rune]*TrieNode)
}
move.next[letter] = &TrieNode{}
}
move = move.next[letter]
move.passCount++
}
move.end = true
}
func (t *Trie) Search(word string) bool {
move := t.root
for _, value := range word {
if _, ok := t.root.next[value]; !ok {
//没有
return false
} else {
//有
move = move.next[value]
}
}
if move.end {
return true
}
return false
}
func main() {
searchStr := []string{"abc", "ac", "c"}
trie := NewTrie()
for _, value := range searchStr {
trie.Insert(value)
}
res := trie.Search("ac")
fmt.Printf("%v", res)
}数组
总结
- 283 数组挑出2个阵营
- 75 数组挑出3个阵营
283. 移动零
考虑边界
输入：[1]
输出：[1]方式一：时间复杂度o(n)
挑出非零值，由于[0,j-1]都是非零值，所以手动将[j,最后]补零
js
var moveZeroes = function(nums) {
//i能按照顺序一直把非零的数放到最前面，这会导致前面的都是非零值，j记录了[0,j-1]都是非零值
let j=0
let len=nums.length
for(let i=0;i<len;i++){
if(nums[i]!==0){
nums[j]=nums[i]
j++
}
}
for(;j<=len-1;j++){
nums[j]=0
}
return nums
};方式二：双指针法。时间复杂度o(n)，但是只循环一次
right按数组顺序遍历，找到第一个不为零的（right前都是零）和前面的零交换。交换后，left向后移1位，表示[0,j-1]都是交换过去的非零值
js
var moveZeroes = function(nums) {
const len=nums.length
let left=right=0
for (;right<len;right++){
if (nums[right]!==0){
let temp=nums[right]
nums[right]=nums[left]
nums[left]=temp
left++
}
}
};75. 颜色分类
双指针法
js
var sortColors = function(nums) {
// 利用快排的思想
// [0,left) 都是0
// [left,i) 都是1 (i是从0开始++的，s[i]相当于视口，判断其值并放入对应区间)
// (right,nums.length] 都是2
function swap(nums,left,right){
temp=nums[left]
nums[left]=nums[right]
nums[right]=temp
}
let left=0,right=nums.length-1
let i=0
while(i<right){
if(nums[i]===0){
swap(nums,left,i)
left++
// 换到i的值一定是 1，可以放心++
i++
}
if(nums[i]===1){
i++
}
if(nums[i]===2){
// 交换
swap(nums,i,right)
right--
// 注意这里没有i++，换到i的值有可能还是2
}
}
};167.两数之和 II - 输入有序数组
循环解决
js
var twoSum = function(numbers, target) {
let len=numbers.length
for(let i=0;i<len;i++){
for(let j=0;j<len;j++){
if(numbers[i]+numbers[j]===target&&i!==j){
return [i+1,j+1]
}
}
}
};二分法
题目强调有序数组
1.两数之和
js
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
let m={}
for(let index in nums){
let curItem=nums[index]
if(m[target-curItem]!==undefined){
return [index,m[target-curItem]]
}else{
m[curItem]=index
}
}
};209. 长度最小的子数组
滑动窗口
js
350. 两个数组的交集 II
map计数器。原本想要将数据都放入map中计数，最后判断map[key]>0的元素，但是需要考虑下面的情况
text
[1,1,2,3]与 [1,1]
==>[1,1]代码：
js
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var intersect = function(nums1, nums2) {
let res=[]
//将长度小的赋值给num1.这里创建的map也小
if(nums1.length>nums2.length){
[nums1,nums2]=[nums2,nums1]
}
let map={}
//用num1建立计数器
for(value of nums1){
if(map[value]){
map[value]++
}else{
map[value]=1
}
}
//遍历nums
for(let value of nums2){
if(map[value]>0){ //num2中元素在map中有
map[value]-- //计数器减1
res.push(value) //加入res
}
}
return res
};88. 合并两个有序数组
双指针
js
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function(nums1, m, nums2, n) {
let i=m-1,j=n-1
let lateIndex=n+m-1
while(i>=0&&j>=0){
if(nums1[i]>nums2[j]){
nums1[lateIndex]=nums1[i]
i--
}else{
nums1[lateIndex]=nums2[j]
j--
}
lateIndex--
}
//num2剩下了
while(j>=0){
nums1[lateIndex]=nums2[j]
lateIndex--
j--
}
};LCR 007. 三数之和
想要用指针，数组先有序
for循环，每次固定一个数据。x[左指针.....右指针]。两个指针对撞
特征：数组+有序
js
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function (nums) {
const len = nums.length;
//1、从小到大
num = nums.sort((a, b) => {
return a - b;
});
let left, right;
let res = [];
//2、例子：[1,1,1] i是第3个数，left=i+1就是第四个数，会出现数组越界。所以遍历到【0，len-2】
for (let i = 0; i < len - 1; i++) {
//3、重复跳过
if (i > 0 && nums[i] === nums[i - 1]) {
continue;
}
left = i + 1;
right = len - 1;
while (left < right) {
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
} else {
res.push([nums[i], nums[left], nums[right]]);
left++;
right--;
//3、 处理左指针元素重复的情况
while (left < right && nums[left] === nums[left - 1]) {
left++;
}
//3、 处理右指针元素重复的情况
while (left < right && nums[right] === nums[right + 1]) {
right--;
}
}
}
}
return res;
};905. 按奇偶排序数组
347. 前 K 个高频元素
暴力
js
var topKFrequent = function(nums, k) {
// hash计数
let hash={}
for(let value of nums){
if(!hash[value]){
hash[value]=1
}else {
hash[value]++
}
}
//[ [key,value],.... ]
let entriesList= Object.entries(hash)
entriesList.sort((a,b)=>b[1]-a[1]) // 按次数从大到小排序
return entriesList.slice(0,k).map(item=>item[0]) // 截取前k个，返回值
};前k个，可以用堆实现，时间复杂度o(nlogn)，但是JS中需要自己实现堆
692. 前K个高频单词
js
var topKFrequent = function(words, k) {
// hash计数
let hash={}
for(let value of words){
if(!hash[value]){
hash[value]=1
}else {
hash[value]++
}
}
//[ [key,value],.... ]
let entriesList= Object.entries(hash)
entriesList.sort((a,b)=>{
if(b[1]===a[1])
return a[0].localeCompare(b[0])
// 如果 string 在字典顺序上位于 compareString 之前，则返回负数
return b[1]-a[1]
}) // 按次数从大到小排序
return entriesList.slice(0,k).map(item=>item[0]) // 截取前k个，返回值
};933. 最近的请求次数
其实这里是双端队列
js
RecentCounter.prototype.ping = function(t) {
this.queue.push(t)
while(this.queue[0]<t-3000){
this.queue.shift()
}
return this.queue.length
};622. 设计循环队列
数据结构课本讲过
核心：front与rear指针重合时，无法区分是空还是满。所以，需要空出来一个位置。长度为n的循环队列，使用长度n+1的数组存储
- 空 front=rear，
- 满 front=（rear+1）%n，n是长度
560. 和为 K 的子数组(前缀和)
前缀和一般需要补一个0
js
var subarraySum = function(nums, k) {
// 前缀和 [x1,x2,x3,x4,x5] ===> (x1+x2+x3+x4) - (x1+x2) 如果两个前缀和的差，是k就代表 [x3,x4]一个解
// 等价于 前缀和-k=另一个前缀和
// 例子 [1,1] k=2; 符合条件，但是 前缀和(1+1)-k(2) = 0,0不是前缀和，所以需要补一个默认的前缀和0（这个边界好难啊！！！）
let prefixSum=0
let count=0
let record={0:1}
// 1
for(let num of nums){
prefixSum+=num
if (record[prefixSum-k]){
count+=record[prefixSum-k]
}
if (!record[prefixSum]){
record[prefixSum]=0
}
record[prefixSum]++
}
return count
};189. 轮转数组
就朴素的想法：拼接新数组，但是注意在注释里要求直接改nums数组不必
有两个坑：
- k可能比数组长度还大
- 给参数num复制指向了新的数组，并不是修改原num数组
js
//【错误代码】
// 注意用例：nums =[1,2] k=3
var rotate = function(nums, k) {
nums = [...nums.slice(-k),...nums.slice(0,-k)]
};正确解法：
js
var rotate = function(nums, k) {
// 对k取余
let offset=k % nums.length
let newNums = [...nums.slice(-offset),...nums.slice(0,-offset)]
// for循环改原数组
for(let index in newNums){
nums[index]=newNums[index]
}
};栈
单调栈的特征：
739. 每日温度
单调栈思路：及时去掉无用数据，保持栈内元素单调有序
js
var dailyTemperatures = function(temperatures) {
let n=temperatures.length
let stack=[]
let res=[]
for (let i=0;i<n;i++){
// 第一次，stack没有数据，直接跳过while，将数据push进去
while (stack.length&&stack[stack.length-1].value<temperatures[i]){
const {index,value}= stack.pop()
res[index]=(i-index)
}
stack.push({index:i,value: temperatures[i]})
}
// 最后栈里还可能有剩余
// 例如输入：3 1 。 stack=[3,1]
while (stack.length!==0){
const {index,value}= stack.pop()
res[index]=0
}
return res
};42. 接雨水
栈内元素单调递减，遇到4时开始接雨水
js
var trap = function(height) {
// 递减
let stack=[]
let n=height.length
let res=0
for (let i=0;i<n;i++){
const curValue = height[i]
// 遇到大于栈顶的元素，循环出栈，接雨水
while (stack.length&&curValue>=stack[stack.length-1].value){
const {index,value} = stack.pop()
// 需要 前前个元素，所以这里判断了栈中是否还有元素
if (stack.length===0){
break
}
const {index:preIndex,value:preValue} = stack[stack.length-1]
// 注意这里的 (i-preIndex-1)， 存在疑问，为啥不是 (i-index)
res+= (i-preIndex-1) * (Math.min(preValue,curValue)-value)
}
// 入栈
stack.push({index:i,value:curValue})
}
return res
};20. 有效的括号
js
var isValid = function(s) {
let stack=[]
for(let i=0;i<s.length;i++){
if(s[i]==='('||s[i]==='{'||s[i]==='['){
stack.push(s[i])
}
if(s[i]===')'&&stack.pop()!=='('){
return false
}
if(s[i]==='}'&&stack.pop()!=='{'){
return false
}
if(s[i]===']'&&stack.pop()!=='['){
return false
}
}
// 最后栈为空，才是有效的串
return stack.length===0?true:false
};简化下
js
var isValid = function(s) {
let pairs=new Map([
['(',')'],
['{','}'],
['[',']']
])
let stack=[]
for(let i=0;i<s.length;i++){
if(pairs.has(s[i])){ // 左括号
stack.push(s[i])
}else{// 右括号
if(stack.length===0||pairs.get(stack[stack.length-1])!==s[i]){
// 特别注意：当输入为)时，栈里为空，取栈顶会报错
return false
}
stack.pop()//栈里有数据，且栈顶和右括号匹配上，这时候就pop
}
}
return stack.length===0?true:false
};232. 用栈实现队列
js
var MyQueue = function() {
this.stack1=[]
this.stack2=[]
};
/**
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
this.stack1.push(x)
};
/**
* @return {number}
*/
MyQueue.prototype.pop = function() {
if(this.stack2.length===0){
while (this.stack1.length!==0){
this.stack2.push(this.stack1.pop())
}
}
return this.stack2.pop()
};
/**
* @return {number}
*/
MyQueue.prototype.peek = function() {
if(this.stack2.length===0){
while (this.stack1.length!==0){
this.stack2.push(this.stack1.pop())
}
}
const res=this.stack2.pop()
this.stack2.push(res)
return res
};
/**
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
return this.stack1.length===0&&this.stack2.length===0
};字符串
涉及回文，可以优先思考使用left、right指针指向字符串的两侧
通过 while限制条件，满足条件可以缩小范围
直到left、right相遇为止（也可能是其他条件结束）
5. 最长回文子串
暴力枚举法：
js
/**
* @param {string} s
* @return {string}
*/
var longestPalindrome = function(s) {
// 校验是否为回文子串
function validPalindrome(s,left,right){
while (left<=right){//注意：等于情况
if(s[left]!==s[right]){
return false
}
left++
right--
}
return true
}
// 最大回文子串长度
let maxCount=1// 一个字母，也是一个回文子串。所以maxCount初始为1
// 最大回文子串开始索引
let begin=0
for(let i=0;i<s.length-1;i++){// 注意：这里到倒数第二位为止
for(let j=i;j<s.length;j++){
if(validPalindrome(s,i,j)){
let span=j-i+1
if(span>maxCount){
maxCount= span
begin=i
}
}
}
}
return s.slice(begin,begin+maxCount)
};中心扩散法：有对称性的可以用
js
var longestPalindrome = function(s) {
// xyx（回文串为奇数） 、 xx（回文串为偶数） 两种情况
// 最大回文子串长度
let maxCount=1// 一个字母，也是一个回文子串。所以maxCount初始为1
// 最大回文子串开始索引
let begin=0
let n=s.length
// 从中心扩展开
function h(left,right){
// (left>=0||right<=n-1) 防止溢出数组
while((left>=0||right<=n-1) && s[left]===s[right]){
if(right-left+1>maxCount){
maxCount=right-left+1
begin=left
}
left--
right++
}
}
for(let i =0;i<n;i++){
// 假设i为最长回文子串的中心
// 如果为奇数
h(i-1,i+1) // i=0时，i-1溢出边界；i=n-1时，i+1溢出边界；都需在h中处理
// 如果为偶数
h(i,i+1)
}
return s.slice(begin,begin+maxCount)
};动态规划法：
状态转移方程：
js
// 初始：i指向target数组最左侧，j从i到target.length
// dp[i][j] 表示 i~j 之间是否为回文子串
dp[i][j]= target[i]===target[j]&&(j-i<=1||dp[i+1][j-1]) //j-i<=1 表示i、j之间只有一个数 + i、j指向一个数，直接算为回文680. 验证回文串 II
删除一个如何做？ 验证如果 i~j 之间的字符串不是回文，不要结束，再增加一个判断 即 i+1~j 和 i~j-1判断是否为回文
这个比较简单的点在于最多删除一个。301题难度高，是因为不限制删除个个数
js
var validPalindrome = function(s) {
// 是否为回文字符串
function isPalindrome(s,left,right){
while (left<=right){
if(s[left]!==s[right]){
return false
}
left++
right--
}
return true
}
let left=0,right=s.length-1
while (left<=right){
// 找到第一个不相等的，删除这个。计算剩下的是否为回文字符串
if(s[left]!==s[right]){
// 这里left+1、rigth-1可能会越界，但是这种情况只有长度为1时会发生，s[0]一定等于s[0]，不会进入这个逻辑里；
// 只要长度大于1，left+1、rigth-1的范围就会向内缩
return isPalindrome(s,left+1,right)||isPalindrome(s,left,right-1)
}
left++
right--
}
return true
};32. 最长有效括号
错误解法：这种解法不是求最长的子串，子串需要连续
用例："()(()"，代码输出4，实际结果为2
var longestValidParentheses = function(s) {
let stackList=[]
for(let i=0;i<s.length;i++){
if(s[i]==='('){ // 遇到（
stackList.push('(')
}else {//遇到 ）
if(stackList.length>0&&stackList[stackList.length-1]==='('){
stackList.pop()
}else{
stackList.push(')')
}
}
}
return s.length-stackList.length
};解答：
js
var longestValidParentheses = function(s) {
// 栈是做括号匹配的好帮手，但是我们需要找到合法的连续子串，栈无法记录是否连续
// 这里我们使用
// 1、栈，入栈元素为s中字母的索引。（ s[index]才能获取实际元素 ）
// 2、辅助数组asset=[0,1,1,1,0]，1表示可以匹配的括号，0表示不可匹配的括号
let stack=[]
let asset=[]
for (let i=0;i<s.length;i++){
if(s[i]==='('){
stack.push(i)
asset[i]=0
}else{
// 这里比较绕，如果当前是 ），如果栈顶是（，则直接出栈
let tackTop=stack[stack.length-1] // 栈里是字符串索引
if(i>=1&&s[tackTop]==='('){
stack.pop()
asset[i]=1
asset[tackTop]=1
}else{
stack.push(i)
asset[i]=0
}
}
}
let maxCount=0
let temp=0
for (let i=0;i<asset.length;i++){
if(asset[i]===1){
temp++
maxCount=Math.max(maxCount,temp)
}else {
temp=0
}
}
return maxCount
};动态规划解法：略
301. 删除无效的括号（难度大，跳过）
返回所有最优的解
bfs 广度优先遍历
视频：https://xiaochen1024.com/series/6196129fc1553b002e57bef5/6197453ddafc4b002e653728 第一个题
387. 字符串中的第一个唯一字符
js
var firstUniqChar = function(s) {
// 哈希计数
// 因为这个题是返回索引，并不是字符。所以map的value除了计数外还有存索引
let m= new Map()
for(let i=0;i<s.length;i++){
if(m.has(s[i])){
let {count,index}=m.get(s[i])
m.set(s[i],{
count:count+1,
index:index+','+i
})
}else {
m.set(s[i],{
count:1,
index:i
})
}
}
//
for(let value of m.values()){
if(value.count===1){
return value.index
}
}
return -1
};14. 最长公共前缀（待补充前缀树解法）
横向扫描：
js
var longestCommonPrefix = function(strs) {
// 为啥排序? 用例： ['abc','ab']，我们应该以最短的作为基准，在最后return sortList[0]是返回的是应该是ab
const sortList=strs.sort((a,b)=>a.length-b.length)
let minLen=200
for (let i=0;i<sortList.length;i++){
minLen=Math.min(minLen,sortList[i].length)
}
for(let j=0;j<=minLen;j++){//索引位置
let temp=''
for(let i=0;i<sortList.length;i++){//遍历所有子元素
if(i===0){
temp=sortList[0][j]
//0或1个元素情况： ['']结果'' 、 ['a']结果'a'的情况
if(sortList.length<=1){
return sortList[0]
}
}else{
if(temp!==sortList[i][j]){
return sortList[0].slice(0,j)
}
}
}
}
return sortList[0]
};前缀树（字典树）
gin框架的路由使用的就是前缀树
js
151. 反转字符串中的单词
这中解法依赖于JS中存在的trim函数，去除首尾空格
slplit函数分割
js
"1 2".split(" ") // ['1','2']
"1 2".split(" ") //1与2之间两个空格， ['1','','2']解法：
js
var reverseWords = function(s) {
// 这里需要先把字符串首尾的空格去掉。
// 例如：输入" a b c"，如果不加trim，a不是arr中的第一个元素，无法命中if(i===0)逻辑，最后结果会多一个空格： "c b a "
const arr=s.trim().split(' ')
let res=''
for (let i=arr.length-1;i>=0;i--){
if(arr[i]===''){
continue
}
if(i===0){
res+=arr[0].trim()
}else {
res+=`${arr[i].trim()} `
}
}
return res
};快慢指针
js
var reverseWords = function(s) {
s=s.trim()
let resArr=[]
let left=s.length-1
let right=left
while(left>=0){
while (left>=0&&s[left]!==' '){
left--
}
resArr.push(s.slice(left+1,right+1))
while (left>=0&&s[left]===' '){
left--
}
right=left
}
// "xxx yyy zzz"，由于最后一个单词没有空格，其他单词有尾空格，还需要判断，不如直接用join
return resArr.join(' ')
};557. 反转字符串中的单词 III
解答：
js
var reverseWords = function(s) {
let res=[]
let arr=s.split(' ')
arr.forEach(item=>{
res.push(item.split('').reverse().join(''))
})
return res.join(' ')
};双指针
js
var reverseWords = function(s) {
let len=s.length
let left=0,right=0
let res=''
function reverseStr(s){
return s.split('').reverse().join('')
}
while (right<=len-1){
while (right<=len-1&&s[right]!==' '){
right++
}
res+=reverseStr(s.slice(left,right))
while (right<=len-1&&s[right]===' '){
right++
res+=' '
}
left=right
}
return res
};1143. 最长公共子序列
动态规划
js
dp[i][j] 表示 `text1从第一个到第i个字符` 与 `text2从第一个到第i个字符` 最长公共子串的长度有两种情况： 关键是text1与text2的下一个字符，是否一样。
- 一样的话，公共子序列个数+1
- 不一样的话，需要比较两个情况哪个大
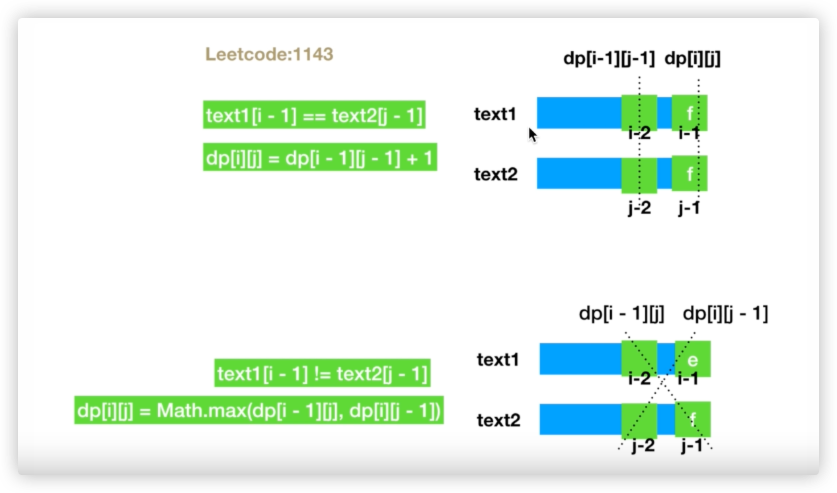
解法：与图的索引有些出入，但是思路一致
js
var longestCommonSubsequence = function(text1, text2) {
dp=new Array(text1.length).fill(0).map(()=>new Array(text2.length).fill(0))
// 初始值
if(text1[0]===text2[0]){
dp[0][0]=1
}
// test1[0]逐一与test2的每一个元素对吧，发现有一样的，后面就都是1了
for(let i=0;i<text2.length;i++){
if(text1[0]===text2[i]){
while (i<text2.length){
dp[0][i]=1
i++
}
break
}
}
for(let i=0;i<text1.length;i++){
if(text1[i]===text2[0]){
while (i<text1.length){
dp[i][0]=1
i++
}
break
}
}
for(let i=1;i<text1.length;i++){
for (let j=1;j<text2.length;j++){
// 这个判断有关很严重的问题
// 第二次循环 i=2，j=1时，
if(text1[i]===text2[j]){
dp[i][j]=dp[i-1][j-1]+1 // 需要初始值dp[0][0]
}else {
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])// 需要初始值dp[1][0]、dp[0][1]
}
}
}
return dp[text1.length-1][text2.length-1]
};
longestCommonSubsequence('ezupkr','ubmrapg')115. 不同的子序列
js
dp[i][j] 表示 s[0~(i-1)]包含t[0~(j-1)]的个数
情况1：s[i-1]!==t[j-1]
dp[i][j]=dp[i-1][j] // 那直接扣掉s[i-1]对结果一定影响都没有，例子： ab与a，第一个串扣掉b
情况2：s[i-1]===t[j-1]
s[0~(i-1)]包含t[0~(j-1)]的个数分成两种情况:
t[0~(j-1)]包含s[i-1]的有a个 a=dp[i-1][j-1] //s[i]===t[j]，需要一下扣掉两个s[i-1]、t[j-1]
t[0~(j-1)]不包含s[i-1]的有b个 b=dp[i-1][j] // i-1就是扣掉s[i-1]
两种情况加起来就是 dp[i][j] = a+b = dp[i-1][j-1] + dp[i-1][j]解法
js
var numDistinct = function(s, t) {
dp=new Array(s.length+1).fill(0).map(()=>new Array(t.length+1).fill(0))
// 初始值
dp[0][0]=1 // 空字符串包含1个空字符串
for(let i=0;i<=s.length;i++){
// 其实这个在i=0时，已经包含dp[0][0]=1了
// 空字符串在任何字符串中都出现一次
dp[i][0]=1
}
for (let i=1;i<=s.length;i++){
for (let j=1;j<=t.length;j++){
if(s[i-1]!==t[j-1]){
dp[i][j]=dp[i-1][j]
}else {
dp[i][j]=dp[i-1][j]+dp[i-1][j-1]
}
}
}
return dp[s.length][t.length]
};需要注意:
s中第i个字母是s[i-1]，t中第j个字母是t[j-1]
s中前i个字母包含t中前j个字母的个数是 dp[i][j]，也就是dp[0][0]这个位置跳过去了，这是因为考虑了空字符串dp[0][0]是s中空、t中空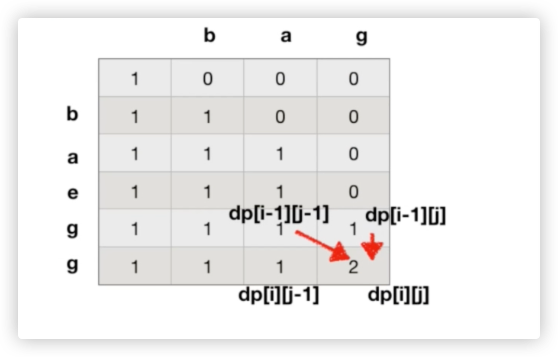
125. 验证回文串
js
var isPalindrome = function(s) {
function isValid(str){
return /^[A-Za-z0-9]+$/.test(str)
}
let left=0,right=s.length-1
while (left<right){ // 注意这里和下面都不能用left<=right ,输入" "，会出现left=0，right=0，符合left<=right进入循环，会出现left++变为1的情况，这样就数组越界了
while (left<right&&!isValid(s[left])){// 遇到过这种情况，注意外层while的条件，在内层改变，这种情况必须在内存限制外层的条件left<right。否则，内层一直left++很有可能内部已经不满足left<=right了
left++
}
while (left<right&&!isValid(s[right])){
right--
}
if(s[left].toLowerCase()!==s[right].toLowerCase()){
return false
}
left++
right--
}
return true
};796. 旋转字符串
暴力
js
var rotateString = function(s, goal) {
let arr=s.split('')
let len=arr.length
for (let i=0;i<len;i++){
if(arr.join('')===goal){
return true
}
arr.push(arr.shift())
}
return false
};官方解答
如果符合条件，那么s长度一定等于goal，且s+s的连续子串一定包含goal
js
var rotateString = function(s, goal) {
return s.length === goal.length && (s + s).indexOf(goal) !== -1;
};
作者：力扣官方题解
链接：https://leetcode.cn/problems/rotate-string/solutions/1398076/xuan-zhuan-zi-fu-chuan-by-leetcode-solut-4hlp/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。844. 比较含退格的字符串
js
var backspaceCompare = function(s, t) {
function actualStr(str){
let res=[]
for (let i=0;i<str.length;i++){
if(str[i]==='#'){
res.pop()
}else{
res.push(str[i])
}
}
return res.join('') // join没有参数，默认使用逗号连接
}
if(actualStr(s)===actualStr(t)){
return true
}
return false
};394
排序算法
冒泡
js
function bubbleSort(arr) {
let len = arr.length;
for (let i = 0; i < len ; i++) {
for (let j = 0; j < len - 1 - i; j++) {
// 比较相邻元素，如果顺序错误就交换
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
}
return arr;
}快速排序
js
function quickSort(arr, left, right) {
if (left>=right){
return
}
let pivotIndex= partition(arr, left, right)
quickSort(arr, left, pivotIndex-1)
quickSort(arr, pivotIndex+1, right)
}
function partition(arr,left,right){
let l=left
let r=right
// 确定中间位置，基于中间位置不停左右交换
let midIndex = Math.floor((l + r) / 2)
let pivot = arr[midIndex]
// 当左侧小于等于右侧则表示还有项没有对比，需要继续
while (l <= r) {
// 当左侧小于基准时查找位置右移，直到找出比基准值大的位置来
while (l <= r && arr[l] < pivot) { // 当操作while条件中的变量时，必须加上while条件，否则会出现不符合最外层while的情况
l++
}
// 当前右侧大于基准时左移，直到找出比基准值小的位置来
while (l <= r && arr[r] > pivot) {
r--
}
if(l <= r){
// 数据交换，小的交换到基准左侧，大的交换到右侧
[arr[l], arr[r]] = [arr[r], arr[l]]
l++
r--
}
}
// arr[l]=pivot
return l // 返回基准值
}
const arr= [3,2,5,1,6]
quickSort(arr,0,arr.length-1)
console.log(arr)位运算
其他类型
1. 两数之和
非常绕，需要仔细想想
js
var twoSum = function(nums, target) {
let count={}
// key = target-数组元素A，value = 是数组元素A索引
// 元素B在count有，就是元素B与某元素之和是target
for (let index in nums){
let value=nums[index]
if (count[value]){
return [index,count[value]]
}
count[target-value]=index
}
};49. 字母异位词分组
这里补充下split、join的坑
js
// 一定得写参数''，被坑了好几次了
"abc".split() // ['abc']
"abc".split(' ') // ['abc']
"abc".split('') // ['a', 'b', 'c']
// 一定得写参数''，完了写参数居然是默认逗号拼接，被坑了好几次了
['a', 'b', 'c'].join() // 'a,b,c'
['a', 'b', 'c'].join('') // 'abc'js
var groupAnagrams = function(strs) {
const record={}
for (let word of strs){
const sortedWord= word.split('').sort().join('')
if (!record[sortedWord]){
record[sortedWord]=[]
}
record[sortedWord].push(word)
}
return Object.values(record)
};128. 最长连续序列
我这种用排序做的，不满足题目O(n)的要求。但是写的时候还是遇到很多注意点，所以还是记录下来
js
var longestConsecutive = function(nums) {
const list=Array.from(new Set(nums)).sort((a,b)=>a-b)
console.log(list)
if (list.length<=1){
return list.length
}
let curMaxLen=1
let maxLen=1 // 注意这种 [1,4,5,7] 最大连续长度是1
for(let index=1;index<list.length;index++){
if (list[index] - list[index-1] ===1){
curMaxLen++
maxLen=Math.max(maxLen,curMaxLen)
}else {
curMaxLen=1
}
}
return maxLen
};标准解法
js
var longestConsecutive = function(nums) {
if (nums.length===0){
return 0
}
const numSet=new Set(nums)
let max=1 // 注意：连续字符最小就是1，只要一个元素就是1个连续
for (let num of numSet){
if (numSet.has(num-1)){
// 看下num的前一个是否有，有就代表不是连续序列的第一个
// 不加这个就超时了
continue
}
let offset=1
while(numSet.has(num+offset)){
max=Math.max(max,offset+1)
offset++
}
}
return max
};56. 合并区间
先按每个区间左短点排序，然后能合并的就与结果集末尾合并，不能合并的推入结果集合
js
var merge = function(intervals) {
let len=intervals.length
const sortedList=intervals.sort((a,b)=>a[0]-b[0])
let ans=[sortedList[0]]
for (let index=1;index<len;index++){
const [preStart,preEnd]=ans[ans.length-1]
const [curStart,curEnd]=intervals[index]
if (preEnd >= curStart){ // 能合并。如何能符合if的情况下一直合并
let end=curEnd>preEnd?curEnd:preEnd // [[1,4],[2,3]] ==> [[1,4]] 拼接的第2个数据包含在第1个内
ans[ans.length-1]=[preStart,end]
}else{ // 不能合并
ans.push([curStart,curEnd])
}
}
return ans
};238. 除自身以外数组的乘积
js
var productExceptSelf = function(nums) {
// answer[i]=numsL[i]*numsR[i]
// numsL[i]=nums[0]*...nums[i-1]=numsL[i-1]*nums[i-1]
// numsR[i]=nums[i+1]*...nums[nums.length]=numsR[i-1]*nums[i+1]
const len=nums.length
const numsL=new Array(len).fill(1)
const numsR=new Array(len).fill(1)
const answer=new Array(len).fill(1)
for (let i=1;i<nums.length;i++){
numsL[i]=numsL[i-1]*nums[i-1]
}
for (let i=nums.length-2;i>=0;i--){
numsR[i]=numsR[i+1]*nums[i+1]
}
for (let i=0;i<nums.length;i++){
answer[i]=numsL[i]*numsR[i]
}
return answer
};补充
很多东西都是大学是数据结构学的，但是时间太过久远了，很多东西都忘记了，这里整理下遇到的吧
KMP
https://leetcode.cn/circle/discuss/yCI2iS/
看下面例子：
// |表示匹配上了，x表示没匹配上
abbaabbaaba 总串
||||||x
abbaaba 子串
// 一般思路是:重新从总串[1]开始继续和子串[0]匹配，这样之前总串[0]与[0]比较的前6位相等的计算就浪费了。可以看下动图
abbaabbaaba 总串
abbaaba 子串
// KML思路是尽可能少回退比较
// 第一次匹配上了前6位，这前六位是abbaab，他自己和自己有首位有重叠部分
abbaab
||
abbaab
// 我们直接把
abbaabbaaba
||||||x
abbaaba // 第一次匹配
||
abbaaba // 我们直接子串开头的ab，顶到把"匹配上的串(前6位) 的重叠部分一般思路：
具体实现参考：https://leetcode.cn/circle/discuss/VMJeMU/
Go模版：
js
func KMP(src, pat string) int {
if pat == "" {
return 0
}
ls := len(src)
lp := len(pat)
next := make([]int, lp)
for i, j := 1, 0; i < lp; i++ {
for j > 0 && pat[i] != pat[j] {
j = next[j-1]
}
if pat[i] == pat[j] {
j++
}
next[i] = j
}
for i, j := 0, 0; i < ls; i++ {
for j > 0 && src[i] != pat[j] {
j = next[j-1]
}
if src[i] == pat[j] {
j++
}
if j == lp {
return i - lp + 1
}
}
return -1
}堆(Heap)
https://blog.csdn.net/Tnkle_sone/article/details/129580158
堆一定是完全二叉树，所以可以使用数组数据存储
核心实现：
- 插入节点，向上调整节点
- 出堆（大顶堆为最大值；小顶堆为最小值）
n个节点构成的堆（完全二叉树）调整时间复杂度为o(nlogn)
0
/ \
1 2
/ \
3 4
用数组的索引代表树的节点。实际节点值存储在数组中
节点n
=>父节点 Math.floor((n - 1) / 2);
=>左子节点 n * 2 + 1;
=>右子节点 (n + 1) * 2 = 左节点 + 1;js
/**
* 堆排序
* @param Array array 用于初始化的数组
* @param Function compareFun 自定义比较函数
* @returns {Heap}
* */
class Heap {
constructor(array = [], compareFun = null) {
this.queue = [];
if (compareFun) {
this.compareFun = compareFun;
}
for (let index = 0; index < array.length; index++) {
this.push(array[index]);
}
}
// 默认的比较函数，小顶堆
compareFun(node1, node2) { // node1是父、node2是子节点
return node1 < node2;
}
// 取堆顶数据
front() {
if (this.queue.length == 0) return null;
return this.queue[0];
}
// 出堆
pop() {
if (this.queue.length == 0) return null;
if (this.queue.length == 1) return this.queue.pop();
const top = this.queue[0];
this.queue[0] = this.queue.pop();
this.sink();
return top;
}
// 入堆
push(node) {
this.queue.push(node);
this.swim();
}
//下沉
sink() {
let curIdx = 0;
let minInd = this.getMinInd(curIdx);
while (this.compareFun(this.queue[curIdx], this.queue[minInd])) {
[this.queue[curIdx], this.queue[minInd]] = [
this.queue[minInd],
this.queue[curIdx],
];
curIdx = minInd;
minInd = this.getMinInd(curIdx);
}
}
getMinInd(curIdx) {
let leftInd = curIdx * 2 + 1;
let rightInd = leftInd + 1;
let minInd = leftInd;
if (
rightInd < this.queue.length &&
this.compareFun(this.queue[leftInd], this.queue[rightInd])
)
minInd = rightInd;
return minInd;
}
//上浮
swim() {
let curIdx = this.queue.length - 1;
let fatherIdx = Math.floor((curIdx - 1) / 2); // 注意：只有一个节点的时候，curIdx、fatherIdx都是0
while (this.compareFun(this.queue[fatherIdx], this.queue[curIdx])<0) {
[this.queue[curIdx], this.queue[fatherIdx]] = [
this.queue[fatherIdx],
this.queue[curIdx],
];
curIdx = fatherIdx;
fatherIdx = Math.floor((curIdx - 1) / 2);
}
}
}排序
不用关系原理，知道原理更记不住了。直接硬记：参数顺序之差为从小到大，参数逆序之差为从大到小
js
arr.sort((a,b)=>a-b) // 从小到大
arr.sort((a,b)=>b-a) // 从大到小思考
for循环
在很多题目中，for循环都给我一种很难表达出心里想法的感觉。这主要体现在：
for循环是将固定的逻辑重放多次，而实际编码中并不是每次逻辑都一致
js// 例如1：for循环内部关系是比较 两个元素的关系。第一个元素之前没有其他元素了，所以不能带入比较两个元素的循环逻辑，需要让i=1开始 arr=[x,x,x,x,x] for(let i=1;i<10;i++){ if(arr[i] 与 arr[i-1]) } // 例如2：部分i需要跳过 arr=[x,x,x,x,x] for(let i=0;i<10;i++){ if(i===0){ continue } } // 例如3：for内部结合while，可以将逻辑锁在while中，只有符合了才会再次进入for。参考滑动窗口模版 for(let i=1;i<10;i++){ // while(条件1){ // 处理。 这里不能操作i，i是for循环来操作。如果内部需要操作i，外部也需要使用while } while(条件2){ // 处理 } // xxx }案例：leetcode239
js// 经典滑动窗口模版 var maxSlidingWindow = function(nums, k) { let res=[] let left=right=0 // for 右指针 ， for循环会先把窗口扩大到k，然后触发while维护窗口 for (;right<nums.length;right++){ // while 维护滑动窗口。不断通过left++缩小窗口 while (right-left+1===k){ // [1,2].slice(1,9) 。slice函数第二个参数溢出，也能正常使用 res.push(Math.max(...nums.slice(left,right+1))) // 推动左指针 left++ } } return res };for循环每次都产生结果，会与下次循环产生逻辑关联
案例：leetcode56题的答案，对比下
[[1,3],[2,6],[8,10],[15,18]] ==> [[1,6],[8,10],[15,18]]jsvar merge = function(intervals) { let len=intervals.length const sortedList=intervals.sort((a,b)=>a[0]-b[0]) let ans=[sortedList[0]] // for循环外放置变量ans，在for循环中if...else条件中不断操作ans。 // 这个题在写的时候十分痛苦：我想不到如何在for循环中的，多轮循环都是if成立（连续合并）。直到看到答案恍然大悟，多次连续合并都操作最后一个元素 for (let index=1;index<len;index++){ const [preStart,preEnd]=ans[ans.length-1] const [curStart,curEnd]=intervals[index] if (preEnd >= curStart){ // 能合并。如何能符合if的情况下一直合并 let end=curEnd>preEnd?curEnd:preEnd // [[1,4],[2,3]] ==> [[1,4]] 拼接的第2个数据包含在第1个内 ans[ans.length-1]=[preStart,end] }else{ // 不能合并 ans.push([curStart,curEnd]) } } return ans };
while
理论上for循环是能替代while的，例如go中只有for循环。但是很多情况下，用for替代while看起来不太直观
js
// 双指针维护一段区间
while(left<right){
// 1、内部需要自己维护 left、right的变化
// 每一轮left、right至少有一个要变化，否则while循环每次都成了一样的了
// 2、数组num会一直循环到出现不一样的元素为止
if(num[left-1]===num[left]){
left++
}
}
// 含义同上，但是觉得不太直观
for(;left<right;)案例：leetcode11题的答案，对比下
js
var maxArea = function(height) {
let left=0,right=height.length-1
let maxCapcity=0
while (left<right){
maxCapcity=Math.max((right-left)*Math.min(height[left],height[right]),maxCapcity)
// 看到内部根据条件，维护left、right变化，推动while进入下一次循环
if (height[left]<height[right]){
left++
}else {
right--
}
}
return maxCapcity
};sum与max
例如，在数组[1,2,3]中，统计某些子串的和，最后返回其中最大的和
js
let sum=0
let max=-Infinity
for(xxx){
// sum累加，算出最后的sum
sum+=xx
}
// sam计算完后，计算最大的max
max=Math.max(max,sum)上面的逻辑有一个错误点，例如当数组为[-1]， max错误的计算为0，max应该是-1
如何规避这个问题啊？
从问题分析
动态规划，dfs递归，可以将所有子组合试一遍。从字符串/数组中挑选K个组成子串/子数组，for循环尝试所有可能需要K层，但是for循环层数不能是动态的啊
- dfs子集型就是典型的收集所有可能的方式。尝试每层有 选、不选两中情况
- 如果要求子串/子数组需要连续的。每层有选、不选两中情况，重点是不选是需要重置path，因为不选就是从当前断开了，从下一个开始连续
找子字符串
找s的子串，要求子串不重复且最长 （leetcode3）
滑动窗口：right一直向右扫描，不断将right加入窗口。但是加入窗口前用Set判断是否重复。如果重复就一直收紧left直到与right相同的那个数字被挤出窗口，再把right加入
输入：s = "abcabcbb" 输出：3 // 只求长度，最长abc找s的子串，要求子串包含t且最短（leetcode76）
滑动窗口：right一直向右扫描，不断将right加入窗口。加入窗口后判断是否完全包含t，如果包含了试图收紧left获取最短子串，否则就继续将right加入
输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC"
找子数组
arr中找一个连续的子数组，要求该子数组和最大（leetcode53）
dfs尝试所有连续的答案，滑动窗口也能解决维护窗口和需要大于0，才能添加右元素
arr中找一个子数组（不需要连续），要求该子数组和为K(leetcode560)
与上题一样解法，会出现一种情况无法解决，dfs算出来子数组 [ [-1,0,1],[-1,0,1]]，即
原地处理数组
leetcode283 移动零